|
|
Ebben a cikkben néhány nyugdíjmodellt mutatok be
belülről, azaz leírva az egyenleteket. Mivel nem szakértőknek írok,
nagyon egyszerű modellekre szorítkozom. Az életciklus modellje a
munkában és nyugdíjban töltött időszak hosszának arányában határozza
meg a fogyasztási pálya kisimításához szükséges megtakarítási
hányadost. A tb-nyugdíjrendszerben az állam nemzedékek közötti
megállapodást hoz létre, és így bonyolítja le a megtakarítást. Két
alaptípusa a nyugdíjrendszer két feladatának felel meg: a
keresetarányos rendszer a jövedelempótlást, az alapnyugdíj-rendszer
pedig az időskori szegénység kiküszöbölését tűzi ki célul. A
kötelező tőkésített nyugdíjrendszerek látszólag függetlenítik a
megtakarítást a nemzedékek közti megállapodástól. Az önkéntes
magánnyugdíj-rendszer az adótámogatással próbálja a tücsköket
hangyává varázsolni. A cikk végén kitérünk a jelenleg domináns
tb-nyugdíjak rejtelmeire, valamint idő- és térbeli változataira.
Bevezetés
A modern társadalmakban a nyugdíj a mindennapi élet része. Még
olyanok is érdeklődnek a nyugdíjkérdések iránt, akik általában
közömbösek a közgazdasági kérdésekkel szemben. Különösen a
nyugdíjkorhoz közeledve kérdezik: „mennyi lesz a nyugdíjam, ha 62
éves koromban 39 éves szolgálati idővel nyugdíjba akarok menni?
Mennyivel nő a nyugdíjam, ha még egy évet rádolgozom?”
Mindegyik nyugdíjrendszer túl bonyolult ahhoz, hogy
e kérdésekre egyszerű választ lehessen adni. A válasz – különösen
hazánkban – érzékenyen függ attól, hogy éppen melyik évben vagyunk.
Mennyi az általános korhatár? (2015 decemberében még 62,5 év volt,
2016 óta – egy évig, 63 évre ugrott.) Van-e még előrehozott nyugdíj?
(2011-gyel bezárólag volt, azóta nincs.) Van-e női kedvezmény? (2011
óta van; akinek negyvenéves jogviszonya van, az levonás nélküli
nyugdíjat élvezhet az általános korhatár elérése előtt is.) Hogyan
lehetnek milliós nyugdíjak? (2013-ban megszűnt a nyugdíjplafon,
amely körülbelül 300 ezer forintban maximalizálta a
nyugdíjkorhatáron visszavonulók járadékát.)
Ebben a tanulmányban ilyen és hasonló kérdésekre
próbálok meg válaszolni. Nem törekszem jogászi pontosságra, de
matematikus lévén nem tudok ellenállni az egyszerűbb képletek és
modellek alkalmazásának. Aki tartalmi részletekre kíváncsi, annak
sokkal alaposabb modellekre van szüksége (Bajkó et al., 2015 vagy
Rézmovits, 2015), de akkor a betekintéshez meg kell szereznie a
teljes dokumentációt is. A jelen cikkhez hasonló szinten tárgyalta a
nyugdíjrendszer kérdéseit Augusztinovics Mária (2002) és Simonovits
András (2007), mindkettő e folyóiratban jelent meg. Jó áttekintést
ad a 2010 körüli helyzetről és a véleményekről a Holtzer Péter
(2010) szerkesztésében megjelent NYIKA-kötet. Tankönyvként
szolgálhat Simonovits András 2002-es kötete. Alkalmazkodva a
nemzetközileg uralkodó irányzathoz, Simonovits cikke (2013) az
egyéni és kormányzati döntések optimalizálásán alapul.
A modern gazdaság kialakulása előtt az emberek zöme
nagycsaládokban élt, ahol a relatíve kisszámú öreg ellátásáról a
családjuk gondoskodott. Elvben régóta lehetőség volt arra, hogy a
jobb módúak magánmegtakarítással gondoskodjanak időskorukról (lásd
Balzac: Goriot apó), de ez kivételes eset volt. A modern társadalom
kialakulásával a nagycsaládok fölbomlottak, s ezért jöttek létre a
különféle nyugdíjrendszerek. A fejlett országokban minden dolgozó
fizet nyugdíjjárulékot, és egy bizonyos életkort megérve mindenki
kap öregségi nyugdíjat. Akinek az egészségi állapota annyira
megromlik, hogy képtelen kielégítő keresettel járó munkát végezni,
az rokkantsági nyugdíjat kap. Gyakori, hogy a nyugdíjas (vagy a
járulékfizető) halála után az özvegy és az árva hozzátartozói
nyugdíjat kap. A továbbiakban csak az időskori nyugdíjjal
foglalkozom.
Alapvetően társadalombiztosítási (röviden tb) és
magánnyugdíj-rendszereket különböztetünk meg: az előbbi a társadalom
nagyon széles körére, szinte mindenkire kötelező, és a fiatal és az
idős korosztályok közti társadalmi szerződésen alapul. Az utóbbi
lehet kötelező és lehet önkéntes, és legalábbis formailag a
magánmegtakarításra épül. Más dimenzióban megkülönböztetjük a
felosztó-kirovó és a tőkésített nyugdíjrendszereket. Általában a
tb-nyugdíj felosztó-kirovó, míg a magánnyugdíj tőkésített; de vannak
keresztezések is: például az amerikai vagy a svéd
tb-nyugdíjrendszernek jelentős tartaléktőkéje van, míg a vállalati
nyugdíjpénztárak gyakran jelentős részben felosztó-kirovó alapon
működnek.
A tb-nyugdíj általában életjáradék, azaz az egyén
haláláig jár. Tipikusan ár- vagy bérkövető (indexált), vagy a kettő
kombinációja. A tb-nyugdíjnak két tiszta alakja van: járulékarányos
vagy alapnyugdíj, az előbbiben a havi nyugdíj arányos az életpálya
folyamán befizetett járuléktömeggel, az utóbbi teljesen független
tőle. A gyakorlatban számtalan átmenet van a két forma között.
A ma ismert kötelező magánnyugdíjat Kelet-Európában
és Latin-Amerikában a tb-rendszerből vágták ki. Az angolszász
világban leginkább nagyvállalati alakja ismert, de bizonyos
országokban (például Hollandiában, Svájcban) a dolgozók zöme
vállalati magánpénztárak tagja. Emellett létezik az önkéntes
magánnyugdíj-pénztár, amelyben a részvétel tényleg önkéntes, de a
részvételt a kormányzat adókedvezményekkel ösztönzi.
A cikk további részében vázlatosan áttekintem az
életciklus-elméletet, a tb- és a magánnyugdíj-rendszereket. Az
előbbin belül kitérek a keresetarányos és az alapnyugdíjra, az
utóbbin belül a kötelező és az önkéntes változatra. Kitérek a
tb-nyugdíjrendszerek néhány rejtelmére, végül pedig utalok a magyar
és a külföldi rendszerek sajátosságaira.
Életciklus-elmélet
Mielőtt meg akarnánk érteni a nyugdíjrendszer logikáját, érdemes
megismerkedni az elvontabb életciklus-modellel. Az érthetőség
kedvéért egyelőre eltekintek a családtól, a munkanélküliségtől, a
növekedéstől, az inflációtól és a kamattól. A következő jelöléseket
vezetem be: L = munkába lépési kor, R = nyugdíj-életkor, D =
halálozási életkor, w = évi teljes kereset (bruttó kereset +
munkáltatói járulékok), b = évi nyugdíj.
Ha s-sel jelöljük az évi megtakarítás teljes kereseti hányadát,
akkor életpályája során a munkás ws (R–L) összeget takarít meg,
amelyet D–R nyugdíjas évre kell egyenletesen elosztani. Adódik az
életciklus-modell alapegyenlete, az időskori fogyasztás:
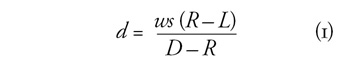
Bár ez az egyenlet nagyon elnagyolt, képes elvi
választ adni néhány fontos kérdésre. Mindenekelőtt, a teljes
keresetem hány százalékát kell megtakarítanom, ha a nettó
keresetemmel [w(1–s)] egyenlő nagyságú nyugdíjat akarok? Válasz:
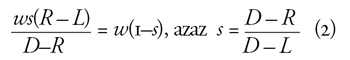
Szavakkal: felnőtt életkorral számolva a
kiegyenlítő megtakarítási hányados egyenesen arányos az
élettartammal, és fordítva arányos a szolgálati idővel. Még
egyszerűbb eredményt kapunk, ha feltesszük, hogy L = D/4 és R =
3D/4: ekkor s = 1/3.
Közelebb hozhatjuk az olvasóhoz a (2) képletet, ha
néhány életszagú értékre kiszámítjuk az általa adott járadékot.
Legyen L = 20 év. Az 1. táblázatból leolvasható, hogy
mennyire érzékeny a végeredmény a két paraméterértékre: 55 és 80 év
közötti időskori fogyasztáshoz 41,7 százalékos megtakarításra van
szükség, 65 és 70 év közöttihez csak 10 százalékra.
|
élettartam (D) |
nyugdíj-életkor (R) |
| 55 |
60 |
65 |
| 70 |
0,300 |
0,200 |
0,100 |
| 75 |
0,364 |
0,273 |
0,182 |
| 80 |
0,417 |
0,333 |
0,250 |
1. táblázat • Megtakarítás (s),
nyugdíj-életkor (R) és élettartam (D)
E fentinél kisebb megtakarítási hányadost kapunk,
ha figyelembe vesszük, hogy a legtöbb esetben a nyugdíj általában
kisebb, mint a nettó kereset (lásd a következő szakaszt). Tovább
módosul az eredmény, ha figyelembe vesszük, hogy a munka során a
dolgozók gyermeket nevelnek, tehát nem csak magukról gondoskodnak.
Külön nehézséget okoz, hogy a dolgozók egy része képtelen
megtakarítani, s emiatt az előtakarékosságot az államnak kell
kikényszerítenie. Hasonló gondot jelent, hogy a pontos élettartam
nem ismert előre, ezért életjáradékot kellene venni. Ez azonban a
magánpiacon meglehetősen drága.
Társadalombiztosítási nyugdíj
(arányos vagy alap-)
Ebben a részben a társadalombiztosítási nyugdíjat elemezzük
részletesebben. Először a makro-, majd a mikrokeretet vizsgáljuk.
Makrokeret
Az s megtakarítási hányad helyett most τ járulékkulcsot írunk.
Egyelőre tegyük föl, hogy a népesség stabil, azaz időszakról
időszakra a dolgozók száma (M) és a nyugdíjasoké (P) párhuzamosan
változik, átlagos keresetük (w*), illetve nyugdíjuk (b*)
párhuzamosan nő. Ekkor (1) helyére a következő egyensúlyi feltétel
lép:
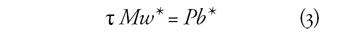
Ezt az egyenletet a következőképpen szokás átrendezni:
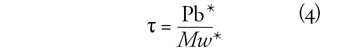
Bevezetve a μ = P/M függőségi hányadost és a β=b/w
bruttó helyettesítési arányt, adódik a tb-nyugdíjrendszer
alapegyenlete; az egyensúlyi járulékkulcs = a függőségi hányados és
a bruttó helyettesítési arány szorzata:
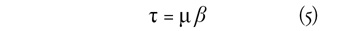
Például az Egyesült Államokban sokkal alacsonyabb
mindkét szorzó, mint hazánkban, ezért alacsonyabb az egyensúlyi
járulékkulcs is. Szemléltető adatokkal: μUS = 0,3 és βUS
= 0,4; azaz τUS = 0,12, míg μH = 0,5 és βH
= 0,6; azaz τH = 0,3.
Pontosabb képet kapunk, ha a nettó helyettesítési
arányra térünk át: βn=b*/v*, ahol – egyelőre elhanyagolva
a személyi jövedelemadót – v = w*(1–τ) a nettó kereset. Ekkor (4)
helyére
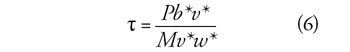
lép, és (5) is módosul:
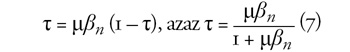
Eddig átlagkeresetekben számoltunk, de a valóságban
egyéni keresetek vannak. A keresetarányos nyugdíjrendszerben ez nem
okoz sok módosítást.
Arányos nyugdíjrendszer
A legegyszerűbb esetben a heterogén kereseteken belül két típust
különböztetünk meg: alacsonyt (L) és magast (H), a megfelelő teljes
keresetek rendre wL és wH, wL < wH
; súlyuk a népességben fL, fH >0, fL
+ fH =1; az átlagos keresetet 1-re normáljuk: fL
wL + fH wH= 1, azaz wL <
1 < wH.
Felírjuk az arányos nyugdíjak egyenletét, ahol
továbbra is β > 0 a bruttó helyettesítési arány:
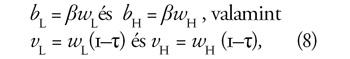
ahol (5), illetve (7) továbbra is érvényes.
Föltesszük, hogy a járulékalapnak nincs plafonja, s ezért
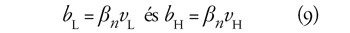
is áll.
Teljesen sima fogyasztási pálya esetén βn = 1,
tehát τM = μ /(1+μ) – ez a maximális járulékkulcs.
Példánkban μ = 1/2, azaz τM = 1/3.
Rögzített várható élettartam esetén finomabb
felbontásban is megismételjük az 1. táblázat számításait. A
2. táblázat a magyar eszmei számlás nyugdíjat adja meg a
nyugdíjas életkor [60, 65] szakaszban. De ehhez szükségünk van az R
éves korban feltételes várható értékre, jele: eR. Egyszerűség
kedvéért csak a férfiakra szorítkozunk, a valóságban azonban a
nőkről sem szabad megfeledkezni. (1)-ben eR = D–R, de a valóságban a
csökkenés lassabb (5 év helyett csak 3), mert közben kilépnek az
állományból a 60-64 éves korban meghaltak. A nettó eszmei nyugdíj
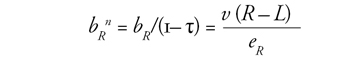
is lassabban nő a nyugdíjba vonulási korral: a τ = 0,25 járulékkulcs
esetén a nettó kereset a 60. korévi 83%-áról 65. korévben „csak” a
114%-ára.
|
nyugdíj-életkor (R) |
várható hátralévő
élettartam
(eR) |
nettó nyugdíj
(bRn) |
| 60 |
16,1 |
0,828 |
| 61 |
15,4 |
0,887 |
| 62 |
14,8 |
0,946 |
| 63 |
14,3 |
1,002 |
| 64 |
13,7 |
1,071 |
| 65 |
13,1 |
1,145 |
2. táblázat • Eszmei nettó nyugdíj – várható hátralévő
élettartam – nyugdíjéletkor
A mélyebb tudást keresők kedvéért megemlítjük, hogy ez a számítás
figyelmen kívül hagyja, hogy a később nyugdíjba vonulók várhatóan
tovább élnek, és nagyobb a keresetük (Simonovits, 2002 és Molnár et
al., 2015). Augusztinovics Mária és Köllő János (2007) hívta föl a
figyelmet arra, milyen fontos az átmeneti gazdaságokban a töredezett
munkapiaci pálya és a nyugdíj kapcsolata.
Alapnyugdíj-rendszer
Most a másik tiszta változatot vizsgáljuk: az alapnyugdíjat, amely
független a keresettől. Legyen az alapnyugdíj b0,
amelynek segítségével (5) átalakul: τ = μ b0. Az
egyszerűség kedvéért elhanyagoljuk a megtakarítást, és így írjuk föl
a fiatal- és időskori fogyasztást:
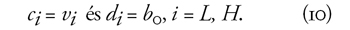
Degresszió
További bonyodalom, hogy a kormányzat az arányos rendszert gyakran a
kis keresetűek javára torzítja: degressziót alkalmaz. Ahány ország
és ahány év, annyiféle degresszió. Mi az elvileg legegyszerűbb
degressziót alkalmazzuk, amikor az arányos (bp) és az alapnyugdíjat
(b0) lineárisan keverik, s a keverés súlya α és 1– α, 0 ≤
α ≤ 1.
A lineárisan degresszív nyugdíj képlete:
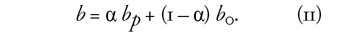
Numerikus szemléltetésünkben a keresetek értéke wL
= 1/2; wH = 2 és fL = 2/3; fH =
1/3, az átlagkereset éppen 1. A 3. táblázat a (11)-beli
degressziót mutatja be különböző súlyok mellett, τM =1/3.
Ha az alaprendszernek nulla a súlya (α = 1), akkor a nyugdíjak
arányosak a bruttó keresettel; ha alaprendszer van (α = 0), akkor
mindkét nyugdíj 2/3. Középen a két nyugdíj aránya 2:1.
| az arányos
rendszer súlya (α) |
kisebb nyugdíj
(bL) |
nagyobb nyugdíj
(bH) |
| 1,0 |
0,333 |
1,333 |
| 0,5 |
0,500 |
1,000 |
| 0,0 |
0,667 |
0,667 |
3. táblázat • Lineáris degresszió és a
nyugdíjak
Kötelező tőkésített nyugdíjrendszerek
A tb-nyugdíjrendszerről szóló részben hallgattunk a fiatalkori
megtakarításról (si). A tőkésített nyugdíjrendszer
bevezetésével ez a kényelmes helyzet megváltozik, és a
megtakarítással is foglalkozni kell. Most nincs tb-nyugdíj (és szja
sem), ezért a nettó kereset megegyezik a teljes keresettel. Nem is
kell foglalkoznunk a kereseti egyenlőtlenségekkel. Definíció szerint
igaz a következő azonosság:
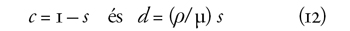
ahol ρ a megfelelő – (1+μ)/2 hosszúságú – időszakra számított
kamattényező. Például az éves kamattényezőt ρ[1]-gyel jelölve, a
(40+20) / 2=30 év esetén ρ= ρ[1]30.
A hagyományos felfogás szerint a kamattényező
nagyobb 1-nél: ρ > 1. Egyes kutatók (például az egyébként úttörő
Martin Feldstein [1985] irreálisan nagy éves kamatlábbal (ρ[1] – 1
=0,114) számol, és ezért nagyon előnyösnek tűnik a tőkésített
rendszer. Ha azonban figyelembe vesszük a befektetések kockázatát és
az életjáradékosítás költségeit, akkor a valóságos kamattényező
jóval közelebb van az 1-hez.
A 4. táblázatban s = τM /2 és τM megtakarítás
hatását ρ[1]=1; 1,05 és 1,1 éves kamattényezővel párosítva mutatjuk
be. Láthatjuk, hogy a 4. (dőlt) sorban, amely a felosztó-kirovó
rendszernek felel meg, a fogyasztás ki van simítva, és értéke 2/3,
addig a legutolsó sorban, a mesés hozamok mellett az időskori
fogyasztás 17,4-szeresen múlja felül a fiatalkorit. Hihetetlen, hogy
a közgazdászok egész serege elfogadott egy ennyire félrekalibrált
modellt.
Önkéntes magánnyugdíj-rendszerek
Az önkéntes nyugdíjrendszer sokak számára népszerűbb, mint a
kötelező. Nem kell kényszert alkalmazni, de a rendszer megmenti a
tücsköket a téli éhhaláltól. Ezt a kedvező megítélést lényegesen
árnyalja, ha nem feledkezünk meg a rendszert megalapozó
adótámogatásról. Persze, ha az adókedvezményben részesülő önkéntes
nyugdíjrendszerben érdemben csak a társadalom krémje vesz részt,
akkor ez a támogatás elhanyagolható, de akkor társadalmilag nincs is
sok hasznossága. Ha viszont tényleg széles körű a rendszer, és
kiterjed a leginkább rászorulókra is, akkor kénytelenek vagyunk az
adóköltséget is mérlegelni. Ezt tesszük a továbbiakban (vö. Király –
Simonovits, 2016).
| éves
kamat-tényező ρ[1] |
megtakarítás (s) |
fogyasztási |
| fiatalkori (c) |
időskori (d) |
| 1,00 |
0,167 |
0,833 |
0,333 |
| 1,05 |
|
|
1,441 |
| 1,10 |
|
|
5,816 |
| 1,00 |
0,333 |
0,667 |
0,667 |
| 1,05 |
|
|
2,881 |
| 1,10 |
|
|
11,633 |
4. táblázat • Tőkésített nyugdíjrendszer –
kamatláb – megtakarítás
Most a heterogén kereseteket kombináljuk a
heterogén előrelátással. Egyszerűség kedvéért feltesszük, hogy a kis
keresetű (wL) rövidlátó és a nagy keresetű (wH)
előrelátó. Továbbra is elhanyagoljuk a kötelező nyugdíjrendszert (τ
= 0), de most a kamatlábat is nullának vesszük (ρ =1). Legyen az
előrelátó megtakarítása sH, a rövidlátóé sL.
Mielőtt a fogyasztási egyenleteket felírnánk, bevezetjük a
támogatási kulcsot: α és a támogatást fedező adó kulcsát: θ. Az
adóegyenlet a következő:
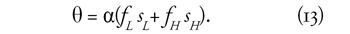
Figyelembe véve, hogy a megtakarítással arányos
kiegészítés a nyugdíjakhoz adódik, új fogyasztási egyenleteink a
következők:
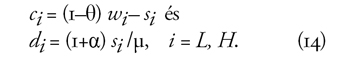
A H típus annyit takarít meg, hogy a fiatal- és az
időskori fogyasztása egymással egyenlő legyen. Ekkor a H esetére
teljesül
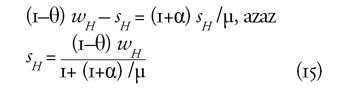
|
|
|
Az L típus ennél gyengébb jellem. Naivan azt
gondolja, hogy mindenki más előrelátó, tehát keresete θ/α részét
takarítja meg, ő ennek csak egy γ részét hajlandó megtakarítani:
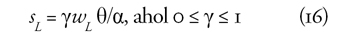
Behelyettesítve (15)–(16)-ot (14)-be, némi számolással adódik az
egyensúlyi adókulcs (és a többi változó):
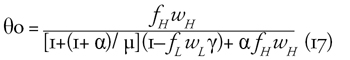
Érdemes még bevezetni a rövidlátó típus veszteségét, amely a
befizetés és a támogatás különbsége: VL= θo wL–
α sL. A további levezetést nem ismertetjük, ehelyett az
5. táblázatban
feltüntetünk néhány numerikus kimenetelt: μ =1/2 és α =1 mellett. Ha
a rövidlátó teljesen aktív (utolsó sor), akkor ő is kiegyenlíti a
fogyasztását, és semmilyen veszteség sem éri az önkéntes nyugdíj
miatt. Ha viszont a rövidlátó passzív (első sor), akkor időskorára
éhen hal. A köztes relatív megtakarítási hajlandóságok átmeneti
kimeneteket adnak.
Ha nem tudjuk emelni a rövidlátók relatív
megtakarítási hajlandóságát, akkor legalább csökkentsük a
támogatást, és vezessünk be egy elég nagyméretű kötelező
nyugdíjrendszert. Ennek a kiszámolását azonban az olvasóra hagyjuk.
A tb-nyugdíjrendszer további részletei
Ebben a szakaszban a tb-nyugdíjak további részleteit fejtjük ki. A
tb-nyugdíjakon belül megkülönböztetjük a kezdő és a már
megállapított nyugdíjakat. Egyszerűsége és nagyobb fontossága miatt
a már megállapított nyugdíjakkal kezdjük.
A már megállapított nyugdíjak indexálása
A legtöbb nyugdíjrendszerben a már megállapított nyugdíjak az előző
évi nyugdíj értékétől függnek. Továbbra is eltekintünk az
inflációtól, de bevezetjük az átlagos reálbér változási tényezőjét
(g t), valamint a naptári időt (t). Ha egy nyugdíjasnak a t-edik
évben bt volt a nyugdíja, akkor az inflációkövetés (árindexelés)
esetén a t+1-edik évben reálértékben ugyannyi lesz a nyugdíja: bt+1
= bt. Ez a rendszer megóvja a nyugdíjasokat az infláció
okozta elszegényedéstől, de gyorsabb reálbér-növekedés esetén a
nyugdíjasokat relatíve elszegényíti, különösen a hosszabb
élettartamúakat (a nőket és a jól kereső férfiakat), illetve a korán
nyugdíjba vonulókat. Csökkenő reálbérek esetén viszont növekvő
terhet rak a dolgozókra.
Ezért is vannak olyan országok, ahol bérkövető
indexálás működik: a t+1-edik évben reálértékben a korábbi gt+1-szerese
lesz a nyugdíja: bt+1 = bt gt+1.
Kompromisszumként alkalmazták és alkalmazzák a kombinált indexálást,
amely részben ár-, részben bérkövető. Legyen ezen indexek súlya π és
1–π, 0 ≤ π ≤1. Például az ún. svájci indexálás esetén a két súly
azonos, azaz π = 0,5.
A kezdőnyugdíjak a mindenkori nyugdíjaknak csak
töredékét (körülbelül öt százalékát) teszik ki, de minden nyugdíj
először kezdőnyugdíj volt, tehát nem lehet elhanyagolni. Eddig az
egész életpályát homogénnek tekintettük, és életkortól (és naptári
évtől) független reálkeresetről beszéltük. Most kénytelenek vagyunk
szakítani e kényelmes gyakorlattal, de csak lépésről lépésre
vezetjük be a bonyodalmakat.
Szolgálati idő, keresetbeszámítás
és általános korhatár
Először tegyük föl, hogy a dolgozó éppen az általános korhatáron
(R*) ment nyugdíjba. Legyen a dolgozó életkora a =L, …, R, és az a
éves kori reálkeresete wa. Emlékeztetünk a korábban használt átlagos
reálkeresetre is, amelyet most wa* jelöl. Ha az a-adik évben
szerzett nyugdíjpontot a saját és az átlagos reálkereset hányadosa
adja: ωa = wa /wa*, akkor az
életpályapontok száma ezek összege. Ha p egy pont értéke, akkor a
pontrendszeres nyugdíj = a pontérték és életpályapontok szorzata:
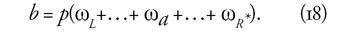
Nem nehéz belátni, hogy ez a rendszer bizonyos
fokig utánozza a tőkésített nyugdíj logikáját, csak itt a
reálkamat-tényező helyébe az átlagos reálkeresetek növekedési
tényezője lép.
Nagyon gyakori, hogy a (18) képlet módosul,
nevezetesen az összes év helyett csak a legutolsó évek (a = A, …,
R*) pontjai szerepelnek: L < A < R*. Ekkor az R*–L-tagú összeg
R*–A-tagúra rövidül, ezt korrigálni kell:
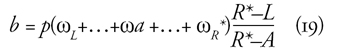
Gyakran nem a beszámítási kor kezdete, A van
megadva, hanem a legkedvezőbb S* időszakot kell figyelembe venni.
(Ezt nem írjuk föl képletben.) A rövidített beszámítási időszak
alkalmazásának több oka is lehet: egyszerűsíti a számítást, kizárja
a munkanélküli időszakot stb., de mindenképpen torzítja a rendszert.
Például a jobb módúak keresete tipikusan gyorsabban nő, mint a
többieké, tehát ezek nyugdíja – a befizetett életpálya-járulékokhoz
képest – magasabb.
Rugalmas korhatár
Eddig feltettük, hogy a dolgozó éppen az általános korhatárt elérve
ment nyugdíjba: R = R*. Hogyan állapítják meg rugalmasan a
nyugdíját, ha dolgozónk ennél korábban vagy későbben megy nyugdíjba?
A tényleges nyugdíj-életkortól függő mértékű büntetést fizet, vagy
jutalmat kap, a módosítás relatív értékének jele: κR,
ahol κR növekvő sorozat, amely éppen az általános
korhatáron veszi föl az 1 értéket: κR*=1. A rugalmas
nyugdíj képlete korlátok között:
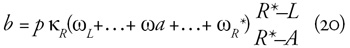
ahol Rm ≤ R ≤RM.
A korrekciós tényező lehet demográfiai: κR = eR
/eR+1; lehet egyszerűen lineáris: κR
=[1+γ (R–R*)], ahol γ > 0, és lehet lefelé kisebb a korrekció, mint
fölfelé.
A lineáris korrekciót mutatja be a
6. táblázat: néhány
szolgálati évre és nyugdíj-korévre szemléltetésül megadja a
megfelelő rugalmas nyugdíjakat, a 2012-ben még érvényes 62 éves
általános korhatárra, egységnyi nettókereset esetére. Például, ha
valaki 38 éves szolgálati idővel és 60 évesen megy nyugdíjba, akkor
a nettó keresete 71,6 százaléka jár neki. A (40, 58) cellában
viszont csak 70,4% áll.
Személyi jövedelemadó hatása
Eddig nem szóltunk a személyi jövedelemadóról (szja), s nemes
egyszerűséggel a nettó kereset kiszámításánál is csak a tb-járulékot
vontuk le a bruttó (vagy a teljes) keresetből. Most is csak nagyon
leegyszerűsítve foglalkozunk azzal, hogyan hat a teljes – bruttó,
illetve a nettó/bruttó kereset különbsége a nyugdíjra (pontosabb
elemzés Cseres-Gergely Zsombor és Simonovits András [2012]
tanulmányában található). Az egyszerűség kedvéért feltesszük, hogy
dolgozónk 2012 után kezdett el dolgozni, és mondjuk 2052 körül megy
nyugdíjba. Csak így tudjuk egyszerűen bemutatni ezt a fontos, de
elhanyagolt hatást. Legyen w a bruttó és v a nettó kereset. Az
egyébként teljesen értelmetlen felosztás szerint megkülönböztetjük a
munkáltatói és a dolgozói járulékkulcsot: τ1 és τ2,
ahol v=(1 – θ – τ2)w. A járulék a bruttó, a járadék a
nettó keresettel arányos:
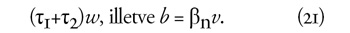
Emiatt az egyensúly feltétele
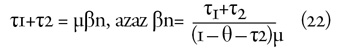
Utolsó egyenletünk szerint, ha egy hozzánk minden
másban hasonlító országban a θ szja-kulcs alacsonyabb, akkor βn-nek
is kisebbnek kell lennie. Pl. jelenleg τ1=0,24 és τ2
= 0,1; azaz amikor 2015-ről 2016-ra θ=0,16-ról 0,15-ra csökkent,
akkor βn egyensúlyi értékének – igaz, csak évtizedek
múlva – 0,81-ról 0,80-ra kellene csökkennie. Ez a korrekció is
hiányzik a hazai nyugdíjképletből.
Nyugdíjplafon
Hasonlóan egyszerűen vizsgálható, hogyan hatott a
nyugdíjjárulék-alap plafonjának 2013-as eltörlése. Az egyszerűség
kedvéért eltekintünk attól, hogy a plafon relatív (nemzetgazdasági
átlagkeresethez viszonyított) értéke 1992 és 2012 között
szeszélyesen ingadozott 1,6 és 3 között. Tegyük föl, hogy a magas
keresetű dolgozó relatív bruttó keresete mindvégig w volt, és annyi
is marad. Legyen wM = 660 ezer Ft, a járulékalap 2012-es
plafonja, a megfelelő vM = (1– θ – τ2) wM a
nettó kereseti plafon, és bM= βn (1– θ – τ2) –
wM = 442 ezer Ft. Helyenként feltesszük, hogy a dolgozó
1988-ban már dolgozott, és w>wM mindvégig teljesült, és t-ben megy
nyugdíjba. Bár 1988 és 1992 között sem volt plafon, de ekkor sokkal
nagyobb volt az szja maximális kulcsa és a degresszió, ezért
figyelmen kívül hagyjuk. Jó közelítéssel korlátozhatjuk a
nyugdíj-degressziót a vM fölötti nettó keresetre, q=0,8 kulccsal. A
plafon nélküli évek a magas nyugdíjat a következőképpen módosítják:
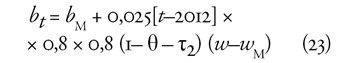
Minél jobban távolodik 2013-tól a nyugdíjba
vonulási életkor, annál jobban nő a magas nyugdíj a plafon
megszüntetése miatt. Két bruttó értékkel számolunk: az első az a
szám, amely mellett 2052 végén a friss nyugdíjas éppen eléri az
egymilliós álomhatárt: w1=2,167 M Ft. A második érték az
első tízszerese: w2=21,67 M Ft. Az alsó kereset esetén
valóban lassú a kitörés: 10 év múlva nyugdíjba vonulók esetén is
csak félmilliós a nyugdíj, és még 25 év múlva is „csak” 3/4 millió.
A felső kategóriában egészen más a helyzet: már 5 év múlva is másfél
milliós nyugdíjasok jelentkeznek, és a folyamat végén, 40 év múlva
9,4 millió Ft is lehet a nyugdíj (7. táblázat).
nyugdíj-év
(t) |
kereset-1
w1=2,167 |
kereset-2
w2=21,67 |
| 2012 |
0,354 |
0,354 |
| 2017 |
0,435 |
1,480 |
| 2022 |
0,515 |
2,606 |
| 2027 |
0,596 |
3,732 |
| 2032 |
0,677 |
4,858 |
| 2037 |
0,758 |
5,985 |
| 2042 |
0,838 |
7,111 |
| 2047 |
0,919 |
8,237 |
| 2052 |
1,000 |
9,363 |
7. táblázat • Nyugdíjév és szupernyugdíj (millió ft/hó),
amikor a plafon megszűnik
Magyarország 1992–
Ezt a cikket magyar olvasóknak írtam, ezért már eddig is utaltam a
hazai nyugdíjrendszer sajátosságaira. Most röviden felsorolom
legfontosabb jellemzőit és időbeli változásait. (Az áttekinthetőség
kedvéért a másodrangúnak ítélt bonyodalmaktól eltekintek.)
1. Magyarországon 1992–1997, illetve 2011 óta a
kötelező nyugdíjrendszer felosztó-kirovó, 1998–2010 között
körülbelül 3:1 arányban felosztó-kirovó, illetve tőkésített rendszer
volt.
2. 1992 óta Magyarországon a kezdőnyugdíjakban az A
beszámítási kor R–5 évről indulva évente egy évvel nő, jelenleg
(1988 óta, illetve későbbi munkába lépéstől kezdve) minden kereset
számít.
3. A kereseti degresszió lényegében már megszűnt,
de a (20) képletben szereplő (R–L)/(R–A) hiperbolikus szolgálati
időskála helyett egy szakaszonként lineáris skála szerepel, amelynek
meredeksége a toldozás-foldozás miatt cikkcakkos, ezt a 8.
táblázat mutatja be.
|
helyettesítés (c) |
szolgálati idő (s) |
| 20 |
25 |
32 |
36 |
40 |
| tényleges |
0,53 |
0,63 |
0,70 |
0,74 |
0,80 |
| arányos |
0,40 |
0,50 |
0,64 |
0,72 |
0,80 |
8. táblázat • Szolgálati időskála
4. Az előrehozott nyugdíjak büntetésmértéke az évek során változott,
2012 óta nincs előrehozott nyugdíj. Fontos kivétel 2011 óta: a Nők
40, amelynek keretében minden nő, akinek legalább negyvenéves
jogviszonya van, teljes nyugdíjjal vonulhat vissza. A halasztott
nyugdíj havi jutalma 0,5%, azaz évente 6%. A 9. táblázat a
6. táblázat számításait fordítja le a 2012-es merev rendszerre.
A 4–6. sort elhagyjuk, mert megegyezik a 6. táblázat megfelelő
soraival. Példánkban a (60, 38) cellában 0 áll, nincs levonással
sújtott előrehozott nyugdíj. Nők esetén viszont a (40, 58) cellában
viszont 70,4 helyett 80% áll.
|
nyugdíj-életkor (R) |
szolgálati idő (s) |
| 36 |
38 |
40 |
42 |
44 |
| 58 |
0 |
0 |
0,80 |
0,84 |
0,88 |
| 60 |
0 |
0 |
0,80 |
0,84 |
0,88 |
9. táblázat • Merev nyugdíjak – szolgálati évek
és nyugdíjéletkorok (nők)
5. A már megállapított nyugdíjak indexálása 1992 és
1999 között bérkövető, 2000 és 2009 között 50–50 százalékban kevert,
majd 2010 óta árkövető. Időnként az indexálás elmaradt a
szükségestől, máskor meghaladta az előírt mértéket.
6. 2003 és 2005 között a 12 havi nyugdíjat plusz 1,
2, majd 3 heti nyugdíj egészítette ki, majd 2006 és 2008 között a
13. havi nyugdíj. 2009-ben a 13. havi nyugdíj megszűnt.
7. 1998 és 2010 között a munkapiacra lépők
általában kötelesek voltak belépni a tőkésített nyugdíjrendszerbe,
az oda fizetett járulék automatikusan csökkentette a tb-járulékot.
Azok a már dolgozók, akik önként átléptek a vegyes rendszerbe,
elvesztették a belépés előtt szerzett tb-jogaiknak az 1/4-ét (mintha
már korábban is a magánrendszerben vettek volna részt, csak a
befizetés elveszett volna.)
Nyugdíjrendszerek térben és időben
Eddig csak érintőlegesen foglalkoztunk a nyugdíjrendszerek idő- és
térbeli változásával. Egy ilyen áttekintő cikkben felesleges volna
részletekbe bocsátkozni, de azért a legfontosabb változatokat
fölvillantjuk.
Tiszta keresetarányos tb-nyugdíjak
Az európai kontinens országainak zömében (csak a legnagyobbakra
szorítkozva: Franciaország, Németország, Olaszország és
Spanyolország, de hazánkban is 1998 előtt és 2011 óta) lényegében
csak a tb-nyugdíjrendszer kötelező, és ez többé-kevésbé
keresetarányos. Míg Franciaországban megfelelő számú gyermek
születik, addig a másik három nagy országban alacsony a születő
gyermekek száma. A közkeletű, de téves vélemény szerint e
rendszerekben gyenge a kapcsolat járulékok és járadékok között, és
ezért a népesség öregedése miatt fenntarthatatlanná válnak. Az
érintett országok kormányai óvatos parametrikus reformokkal
próbálják fenntarthatóvá tenni a rendszert, de közben hajlamosak a
megfelelőségről (adekvátságról) megfeledkezni.
Tiszta tőkésített nyugdíj
A nagy válság és a II. világháború előtt számos országban (köztük
hazánkban is) tiszta tőkésített nyugdíjrendszerek működtek, de ezek
mind tönkrementek. Helyükre mindenütt különféle tb-rendszerek
léptek. Sokáig lehetetlennek tartották a visszatérést a tőkésített
rendszerhez, hiszen az áttérés során évtizedekig külön forrásból
kell fedezni a tb-nyugdíjasok járadékát. 1981-ben Chile újra
bevezette a tiszta kötelező tőkésített magánnyugdíjrendszert.
Hatalmas költségvetési többletet elérve a chilei állam évtizedeken
keresztül képes volt fedezni az áttérés költségeit. Később
megmutatkoztak e rendszer árnyoldalai: túlzottan nagyok voltak a
működési költségek, és megengedhetetlenül sokan maradtak ki a
magánrendszerből és a szándékosan szűkre szabott segélyrendszerből.
Ma már az eredeti tőkésített rendszert jelentős rászorultsági
nyugdíj egészíti ki, és további tb-bővítés várható.
Degresszív tb-nyugdíjak
+ tőkésített nyugdíjak
Az angolszász és a skandináv országokban kisebb-nagyobb degresszív
rendszert egészít ki egy nagyobb-kisebb tőkésített rendszer. Az
egyik véglet Nagy-Britannia, ahol sokáig nagyon szerény, de 1997-től
növekvő vásárlóértékű alapnyugdíjat a dolgozók felénél jelentős
nagyságú magánnyugdíj egészít ki. A másik véglet Svédország, ahol a
tb-rendszer szinte tökéletesen utánozza a magánrendszert, de
jelentős rászorultsági enyhítéssel. Ehhez adódik egy szerényebb
tőkésített rendszer, amelynek kisebbik összetevője kötelező, a
nagyobbik ajánlott.
Keresetarányos tb-nyugdíjak + tőkésített nyugdíjak
Latin-Amerikában és a volt szocialista országok zömében a Világbank
tanácsára megjelentek a vegyes nyugdíjrendszerek. Az eredeti
elképzelés az volt, hogy a tb-pillér kicsiny és degresszív lesz, és
ekkor marad elég hely a tőkésített pillérnek. Az áttérési költségek
csökkentése végett a legtöbb reformkormányzat megfordította a
Világbank sugallta arányokat: a tb-pillér megmaradt dominánsnak.
Emellett a befizetési érdekeltség megerősítése kedvéért a korábban
erősen degresszív tb-rendszer is arányossá vált. A 2008-as válság
hatására azonban mindenütt megrendült a költségvetési egyensúly,
ezért egyes országokban (Szlovákia, Észtország) csak visszafogták,
másutt (Magyarország, Lengyelország) felszámolták a tőkésített
alrendszert. Ez a fordulat látszólag csökkentette a költségvetési
hiányt, de egyéb okok miatt nem mindenütt sikerült megfelelően
csökkenteni az államadósságot (rossz példa Magyarország).
Következtetések
A nyugdíjrendszer időben és térben változó, összetett
transzfermechanizmus. Nem lehet egyik-másik elemét módosítani
anélkül, hogy a többi elemét ne érintsük. Ellentétben más
transzferrendszerekkel, a nyugdíjrendszerek évtizedekre szólnak. Ha
rossz döntést hoz egy kormány, akkor csak nagy nehézséggel lehet a
hibát kijavítani (a 13. havi nyugdíj visszavonása, a Nők 40
reformjától való húzódozás).
A nyugdíjrendszer bonyolultsága lehet az egyik oka annak, hogy a
közgazdasági tankönyvekben kevés teret szentelnek ennek a
rendszernek. Pedig a mai gazdaságban a nyugdíjrendszer fontos, és
megfelelően leegyszerűsítve, jól modellezhető; hiszen ellentétben a
hasonlóan fontos egészségügyi ellátással vagy a közoktatással, a
nyugdíjrendszer közvetlenül pénzről szól.
A felnőtt állampolgárok zöme nemcsak járulékfizető,
hanem járadékos is lesz, és mind a levont járulék, mind a kapott
járadék jövedelmük jelentős része. Érdemes ismerniük a
nyugdíjrendszer működését, és képeseknek kell lenniük
különbségtételre a különféle nyugdíjprogramok között. De még a
politikusoknak (kormánypártiaknak és ellenzékieknek egyaránt) sem
árt, ha legalább nagy vonalakban tisztában vannak a nyugdíjrendszer
titkaival. Ebben próbált segíteni ez a cikk.
Kulcsszavak: nyugdíjrendszerek, modellek, reformok, szja,
nyugdíjplafon
IRODALOM
Augusztinovics Mária (2002): A
nyugdíjrendszerről. Magyar Tudomány. 47, 4, 447–460. •
WEBCÍM
Augusztinovics Mária – Köllő János (2007):
Munkapiaci pálya és nyugdíj: 1970–2020. Közgazdasági Szemle. 54,
június, 529–559. •
WEBCÍM
Bajkó Attila – Maknics A. – Tóth K. –
Vékás P. (2015): A magyar nyugdíjrendszer fenntarthatóságáról.
Közgazdasági Szemle. 62, 1229–1257. •
WEBCÍM
Cseres-Gergely Zsombor – Simonovits András
(2011): A személyi jövedelemadó-reform hatása a tb-nyugdíjakra.
Közgazdasági Szemle. 58, 1029–1044. •
WEBCÍM
Feldstein, Martin (1985): The Optimal
Level of Social Benefits. Quarterly Journal of Economics. 100,
302–320. •
WEBCÍM
Holtzer Péter (szerk.) (2010): Jelentés a
Nyugdíj és Időskori Kerekasztal tevékenységéről. Miniszterelnöki
Hivatal, Budapest
Király Balázs – Simonovits András (2016):
Megtakarítás és adózás egy önkéntes nyugdíjrendszerben: egy
ágensalapú modell felé. Közgazdasági Szemle. közlésre beküldve
Molnár D. László – Hollósné Marosi Judit
(2015): Az öregségi nyugdíjasok halandósága, Közgazdasági Szemle.
62, 1258–1290. DOI:10.18414/KSZ.2015.12. 1258 •
WEBCÍM
Rézmovits Ádám (2015): Nyugdíjkiszámítási
rendszerek összehasonlító vizsgálata. Közgazdasági Szemle. 62,
1309–1327. DOI: 10.18414/KSZ.2015.12.1309 •
WEBCÍM
Simonovits András (2002):
Nyugdíjrendszerek: tények és modellek. Typotex, Budapest
Simonovits András (2007): Nyugdíjmodellek.
Magyar Tudomány. 12, 1527–1533. •
WEBCÍM
Simonovits András (2013): Egyszerű
paternalista transzfermodellek családja. Közgazdasági Szemle. 60,
402–430. •
WEBCÍM
|
|