Internetes vásárlás vagy banki ügyintézés során már mindenki futtatott kriptográfiai alapú algoritmust az internetes böngészőjét használva. Egészen biztosan mindenki hallott már rejtjelezésről (esetleg titkosírás néven irodalmi olvasmányokból), mindenki naponta használ jelszóalapú hitelesítési algoritmust, illetve akár a napi sajtó technikai rovataiban is olvashatott a digitális aláírásról.

A hétköznapokban használt módszerek nagy része mögött tipikusan (sajnos) nem áll bizonyított garancia, biztonságukat a tervezők nagy gyakorlati tapasztalata garantálta. Ez azt jelenti, hogy a konstruált algoritmus (kriptográfiai primitív, illetve protokoll¹) analízise a tapasztalatok szerinti, lehetségesnek vélt támadási módszerek „listájával” szembeni, legtöbbször informális ellenőrzést jelenti. Az ún. modern kriptográfia formális matematikai modellben történő formális bizonyítást céloz meg. Innen származik ezen irányzat másik neve: bizonyított biztonságú kriptográfia. A formális kezeléshez matematikai modellre van szükség. Ennek a modellnek tudnia kell formálisan leírni többek között azt, hogyan definiáljuk egy kriptográfiai algoritmus biztonságosságát, kapcsolatosan a támadó formális modelljét.

Hetven év Shannontól napjainkig

A bizonyított biztonság úttörője Claude Shannon volt. Hetven évvel ezelőtt formalizált, matematikai (információelméleti) modellt adott a szimmetrikus kulcsú rejtjelezés feladatra. Bebizonyította, hogy a one time pad rejtjelező tökéletes abban az értelemben, hogy rejtjelezett üzenethez hozzáférő, a kommunikációs csatornát lehallgató támadó zéró információhoz képes csak jutni, bármekkora számítási kapacitással is rendelkezik (de akkor is, ha a világ végezetéig próbálkozhatna a megoldással). Ez a rejtjelező roppant egyszerű, minden egyes továbbítandó üzenetbithez véletlenül sorsolt kulcsbitet adunk modulo 2, majd a távoli fél ugyanezt a műveletet végzi el a vett bittel, ahol feltétel, hogy azonos kulcsbiteket használjon a küldő és vevő fél.² A módszer hátránya pontosan ezen utóbbi feltétel: ugyanis a véletlen kulcsbiteket az egyik fél generálja, és azt biztonságosan el kell juttatni a másik félhez, azaz valamiféle biztonságos csatornának kell léteznie a két fél között. Ha pedig van ilyen csatorna, akkor megkérdezhetnénk, hogy eleve miért nem azon továbbítjuk magát az üzenetet. Egy gyakorlati szcenárió, amely mellett mégiscsak értelmes a feladat, és kihasználható az említett tökéletesség tulajdonság, az, amikor időben szétválik a kulcsmegegyezés és a rejtjelezés feladat: például a két fél találkozik és kulcsot egyeztet, majd valamely későbbi időpontban ezen kulccsal rejtjelezett üzenetváltást végez. Vegyük észre azt is, hogy a kicserélt kulcsbitek számát nem haladhatja meg a rejtjelezetten küldendő üzenetbitek száma, ami nyilván korlátozza a biztonságosan küldhető üzenetbitek számát. Speciális feladatokban használható csak ez a megoldás, kommerciális tömeges feladatokra nem alkalmas.

Sokáig váratott magára, amíg a bizonyított biztonságú kriptográfiai primitívek következő generációja megszületett. Harmincöt év telt el Shannon úttörő munkáját követően (az 1980-as évek kezdetéig), amikor algoritmuselméleti (számítástudományi) alapokon megszülettek az új matematikai modellek, amelyek alappillérét az egyirányú függvény jelentette. Innen számítjuk a modern kriptográfia indulását. A dolog informális lényegét tekintve arról van szó, hogy Shannon számítási komplexitás korlát nélküli támadója helyett egy reálisabb, csak számítási komplexitásában korlátozott támadó algoritmust futtatni képes ellenfelet tételezünk fel. Konkrétan, véletlen elemeket is felhasználható, az adott feladat biztonsági paramétere bitméretében polinomiális futási idejű (PPT – Probabilistic Polinomial Time), de egyébként tetszőleges támadó algoritmusról van szó. Például a biztonsági paraméter megfelelően nagyra választott értéke mellett kizárjuk, hogy kimerítő keresést végezzen a támadó. A nevezett egyirányú függvény biztosítja (informális megfogalmazásban), hogy a támadó ne tudja megoldani azt a feladatot, hogy a függvény képtere egy tetszőleges eleméhez megadjon illeszkedő ősképtérbeli elemet. Ha már van egyirányú függvényünk, akkor arra építkezve konstruálhatunk bizonyított biztonságú álvéletlen generátort, álvéletlen függvényt és álvéletlen permutációt, ahol az utóbbi a bizonyítható biztonságú szimmetrikus kulcsú blokk rejtjelező modellje. Itt az álvéletlen jelző azt jelenti, hogy a fentiekben említett korlátozott komplexitású algoritmussal vizsgálva az input–output viselkedést, az nem különböztethető meg a valódi véletlen algoritmusétól, például az álvéletlen generátor outputja az azonos bithosszúságú pénzfeldobás-sorozattól. A biztonság bizonyítások technikai módszere az algoritmikus redukció, indirekt bizonyításon belül: mindegyik konstrukció egy, a támadó számára feltételezetten „nehéz” feladatra épül, és azt bizonyítjuk be, hogy amennyiben a konstrukciónk támadható lenne, akkor a nehéz feladat is támadható lenne. Ilyen standard feladat például az egész szám faktorizáció vagy a diszkrét logaritmus számítása. A korszak legnevesebb képviselői között megemlítjük Andrew C. Yao, Leonid Levin, Oded Goldreich, Shafi Goldwasser, Silvio Micali, Michael Luby, Charles Rackoff és Phillip Rogaway nevét. Valamennyien a számítástudomány világhírű képviselői.

A harmadik hullám a 2000-es évekre és napjainkra tevődik. Az elődök munkájára épül, de alapvetően új megközelítést igényelt a kriptográfiai protokollok bizonyított biztonságú módszertana, az univerzális kompozíciós módszertan (UC – Universal Composability Framework) (Pfitzman – Waidner, 2000; Canetti, 2000). Ez a ma ismert legerősebb garanciákat nyújtó technológia a kriptográfiai protokollok moduláris tervezésére és biztonsági analízisére. Ezen módszertan erős támadói környezet mellett kívánja garantálni az adott feladathoz tartozó ideális funkcionalitás realizálását. A szokásos informális analíziseken értelemszerűen túlmutat azzal, hogy bizonyított garanciát nyújt. Más bizonyításos módszertanokkal szemben pedig alapvetően abban, hogy tetszőleges konkurrens futtatási környezetben garantálja az adott protokollpéldány biztonságos szeparálását, immunitását az „ellenséges”, támadó által vezényelt interakciókkal szemben. És mindezt úgy garantálja, hogy ez egy UC-biztonságosnak bizonyított protokoll, moduláris elemként felhasználható tetszőleges más protokoll konstruálásánál, mondhatni ez egy biztonságos, algoritmikus „plug-in technika”. Ennek a máig is tartó hullámnak világhírű képviselői közül megemlítjük Ran Canetti, Birgit Pfitzmann, Hugo Krawczyk, Yehuda Lindell, Boaz Barak és Ivan Damgaard nevét.

Hangsúlyozni kívánjuk, hogy a kriptográfia tudománya igen széles terület, és abban egy szelet a bizonyított biztonság témaköre. A kriptográfia teljességét tekintve jeles hazai képviselői közül megemlítjük Buttyán Levente (protokoll konstrukciók), Csirmaz László (kombinatorika), Ligeti Péter (számítástudomány), Nemetz Tibor (információelmélet), Pethő Attila (elliptikus görbék) és Szabó István (matematikai statisztika) nevét.

E rövid történeti áttekintés után visszakanyarodunk a címben megjelölt témához. Meggyőződésünk, hogy a dolgok közepébe ugrással tudjuk ezt leghatékonyabban megtenni, ebből profitálhat legtöbbet az olvasó, és hogy egy távoli tudományterületet művelő kutató is megérezze, melyek a modern kriptográfia mozgatórugói. E célból néhány alapprobléma lényegét mutatjuk be tömören és a formalizmus minimumon tartása mellett, amelyekre adott válaszok szorosan kapcsolódtak a nevezett tudományterület fejlődéséhez. A következő problémákat emeljük ki:

• Egymásban nem bízó két távoli fél képes-e megbízható közös számítást végezni egymástól eltitkolt (féltett) információikon, ahol a számítás mindkettőjük által megismerendő végeredménye függ a mindkét fél által birtokolt információtól?

• Lehet-e tetszőleges jövőbeli PPT támadó algoritmus ellen biztonsági garanciát nyújtani?

• Önmagában biztonságosnak minősített – különböző tervezőtől származó – két algoritmus kompozíciójának biztonsága garantálható-e?

A tengernyi fontos referencia közül, inkább csak szemelvényként néhányat emelünk ki, kiindulópontokat adva a mélyebben érdeklődő olvasónak. Nem szerénytelenség miatt szerepelnek a szerző saját, alapvetően alkalmazásorientált friss publikációi (Vajda, 2013a,b, 2014, 2015a,b) talán aránytalanul nagy számban e rövid referencialistán, csak némi jogosítvány kívánt felmutatni arra, hogy a taglalt témában itt megszólaljon.

Lehet-e egymástól titkolt információkon megbízható közös számítást végezni?

A modern (bizonyított biztonság igényű) kriptográfia kiinduló alapfeladata a biztonságos függvénykiszámítás problémája volt (Goldreich et al., 1987; Goldreich, 2007; Yao, 1982).

A feladat az, hogy távoli, egymással kommunikációs csatornákon kapcsolatban levő, egymásban meg nem bízó N résztvevő közösen kiszámítson egy y = F(x₁,…,x_N) függvényt, ahol kiindulásképp az i-edik résztvevő és csak ő ismeri az xi inputot, i = 1,…N. Ha a résztvevők támaszkodhatnának egy megbízható harmadik félre, akkor a feladat realizációja arra egyszerűsödne, hogy az egyes résztvevők a megbízható harmadik félnek biztonságos csatornán átadnák titkos információikat, majd a megbízható fél elvégezné a számítást, és a végeredményt kiosztaná a résztvevők között. Talán a legegyszerűbb ilyen függvény két bit XOR-ja,³ azaz N = 2, y = x₁+x₂ mod 2, x₁, x₂{0,1} (1. ábra). Például két résztvevő közösen szeretne egy y véletlen bitet generálni, saját, független generálású x₁, illetve x₂ véletlen bitjéből.

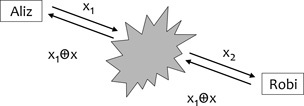
1. ábra • Két bit XOR-jának kiszámítása

megbízható harmadik fél esetén

Tegyük fel, hogy nem támaszkodhatunk harmadik félre. Képzeljük el, hogy Aliz és Robi válnak, és pénzfeldobással, telefonon keresztül kommunikálva szeretnének dönteni közös vagyontárgyaik sorsáról XOR-alapon. Megállapodnak abban a szabályban, hogy ha y = 1 az eredmény, akkor Aliz, ellenkező esetben Robi a nyertes. Kicsit is belegondolva, a probléma az, hogy egyik résztvevő se közölheti a másik féllel elsőként a bitjét, mert akkor a másik hazudhat, hogy a végeredményt a saját javára fordítsa. Például, ha őszinte Aliz pénzfeldobásának eredménye 1, és ezt közli Robival, erre Robi azt hazudhatná válaszként, hogy az ő pénzfeldobásának eredménye is 1, így y = 1+1 = 0 (mod 2) okán Robi biztossá tehetné a győzelmét (ami becsületessége esetén csak 0,5 valószínűségű lehetne).

A feladat bizonyított biztonsággal megoldható. Manuel Blum protokollja az egyik indító alapcikke a modern kriptográfiának (Blum, 1981). A dolog lényegét tekintve, Blum bevezetett egy érdekes részfeladatot, az ún. bitelkötelezés feladatot. Ez azt jelenti a fenti példánkban, hogy Aliz elküld egy bitsorozatot Robinak, amivel elkötelezi magát x₁ bitje mellett anélkül, hogy Robi ebből megtudhatná a kérdéses bitet. Ezután Robi elküldheti nyíltan x₂ bitjét Aliznak, s legvégül Aliz „kinyitja” az elkötelezés információt, anélkül, hogy csalhatna x₁ értéke felől, s ezzel Robi is megismeri az x₁ bitet. Az eredeti biztonságos XOR-számítás feladatot így a biztonságos bitelkötelezés feladatra redukáltuk, amely utóbbira azóta ismerünk biztonságos realizációkat.

Biztonsági garancia tetszőleges jövőbeli támadással szemben?

Ahogy fentebb említettük, a Shannon által analizált one time pad rejtjelező tökéletes védelmet biztosít olyan támadóval szemben, amely lehallgatva a kommunikációs csatornát, olvashatja a rejtjelezett biteket. Ezen feltétel mellett a tökéletes védelem tetszőleges jövőbeli támadó algoritmussal szemben is fennáll. Azonban napjaink hálózati támadója összehasonlíthatatlanul erősebb, mint az egyszerű passzív (lehallgató) típusú támadó.

A támadó a résztvevők közti minden egyes kommunikációs csatornán jelen lehet (MIM – Man-In-the-Middle támadó), lehallgathatja, időlegesen tárolhatja, késleltetheti, aktívan módosíthatja a csatornán haladó valamennyi üzenetet (2. ábra).

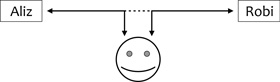
2. ábra • Man-in-the-Middle támadó

Támadás azonban nemcsak a kommunikációs csatornát érheti, hanem a résztvevők azon eszközeit (például számítógépét) is, amelyen a biztonsági algoritmusokat (kriptográfiai protokollokat) futtatják. A legerősebb ilyen, ún. korrumpáló támadó a bizánci típusú dinamikus támadó, amely kriptográfiai protokoll futásának bármely pontján dönthet valamely résztvevő (gépe) korrumpálására, és annak eredményeképpen annak pillanatnyi belső állapotát (például titkos kulcsait) megtudhatja, és a korrumpált résztvevő vonatkozásban a protokolltól eltérő tetszőleges algoritmust futtatva vehet részt a protokoll hátralevő lépéseinek végrehajtásában. Ezenfelül a támadó tetszőleges számú protokollpéldányt futtathat a hálózaton a támadásra célba vett protokollpéldánnyal egy időben ugyanabból vagy tetszőleges, akár ártó szándékú protokollból választva a támadó példányokat.

Lehetséges-e ilyen képességű PPT-támadó esetén bizonyított garanciát adni tetszőleges jövőbeli támadási algoritmus mellett? 

Fentebb említettük, hogy biztonsági bizonyításaink nem klasszikus matematikai bizonyítások, hanem algoritmikus redukciók, ahol általánosan elfogadott feltételezésekkel élünk abban a vonatkozásban, hogy léteznek PPT-támadó számára nem végrehajtható számítási feladatok. Ennek megfelelően, amennyiben ezen feltételezések érvényben maradnak a jövőben is, akkor fennállnak a kérdezett jövőbeli garanciák. Példaként itt a kvantumszámítógéppel történő támadás jövőbeli lehetőségére utalok, amely ha valóban konkrét veszéllyé válik, az több, jelenleg még nehéznek sejtett feladatot könnyen megoldhatóvá tenne, és végveszélybe sodorná számos, ma használatban lévő kriptográfiai protokollunkat (ilyen feladatok az egész szám faktorizáció, illetve a diszkrét hatványozás).

Részfeladatokra bontás és moduláris építkezés

Minél nagyobb méretű egy protokoll (például a protokoll lépéseinek számában), annál nagyobb feladat biztonságának formális bizonyítása. Ezért törekedni kell a részfeladatokra bontásra, azok önálló analízisére. Azt szeretnénk, hogy önmagukban biztonságosnak minősített elemekből építkezve a kompozíció eredménye is biztonságos maradjon. A modulokból összeálló kompozíció lehet alapvetően soros, párhuzamos vagy – általánosan – ezek keveréke. Például klasszikus soros kompozíció a biztonságos csatornát realizáló protokoll esetére a következő: partnerazonosítás → kapcsolatkulcs-csere → rejtjelezett üzenetcsere. Egy másik tipikus példa, amikor egy főprogram szubrutinjaként fut egy modul, jellemzően egy kriptográfiai primitív (például rejtjelező algoritmus, digitális aláíró algoritmus), amelyhez a futás során többször fordul a résztvevő.

Ennek megfelelően fontos igény és tervezési szempont a modularitás. A megközelítés analóg a programtervezésben megszokott modularitással, ahol az egyes modulok programozói interfészének definiálása a kiindulópont, mert ha ez már megvan, ettől kezdve akár független programozók is fejleszthetik a modul tartalmát, ugyanis az egymáshoz való végső csatlakoztatásuk problémamentes lesz. A kriptográfiai modulok interfésze kapcsán kerül elő két alapvető paradigma: az algoritmikus megkülönböztethetetlenség, valamint a szimulációs paradigma.

Az első izgalmas megállapítás az, hogy akár két „durván” különböző eloszlású valószínűségi változó is lehet megkülönböztethetetlen tetszőleges PPT megkülönböztető algoritmus számára. Analógként képzeljünk el két, apró részleteiben különböző képet, amelyeket távolról nézünk, és nem tudjuk az adott távolságból (a kapcsolatosan adódó „felbontásban”) megkülönböztetni. Az algoritmikus feladatban a felbontás finomságának analógja a megkülönböztetést végző algoritmus komplexitás-korlátja. Konkrét példaként az álvéletlen generátort tekintsük: létezik álvéletlen generátor (PRG), amely egy polinomiális futási idejű determinisztikus algoritmus, és amely egy n bites (valódi) véletlen bináris sorozat inputot (magot) p(n) hosszúságú álvéletlen sorozatra nyújt ki tetszőleges p polinom esetén (Blum – Micali, 1984). Például tekintsünk egy kétszeresen hossznövelő PRG-t, azaz ahol p(n)=2n. Ekkor a pénzfeldobással sorsolt 2n hosszú bináris X sorozat algoritmikusan megkülönböztethetetlen lesz a PRG által generált Y 2n bites álvéletlen sorozattól. Vegyük észre, hogy az utóbbi az összes 2n bites sorozatok 22n elemszámú halmazának csak egy elenyésző 2n méretű részhalmazából veszi értékeit (amennyit n bites maggal generálni tudhatunk). Ugyanakkor ezen X és Y változók valószínűségi eloszlásának (statisztikai) távolsága közel maximális (1-2-n), azaz az eloszlások teljesen eltérők.

Ha azonos feladat végrehajtására tervezett két kriptográfiai modul az interfészén keresztül vizsgálva egymástól algoritmikusan megkülönböztethetet-lennek bizonyul, akkor azokat ekvivalensen felhasználhatónak tekintjük. Az „etalon”, amelytől valamennyi, adott feladatra tervezett biztonságos megvalósításának algoritmikusan megkülönböztethetetlennek kell lennie, az az adott feladat ideálisan biztonságos protokollja. Az ideális protokollban valamennyi résztvevő egy megbízható harmadik félen, az ún. ideális funkcionalitáson keresztül kommunikál (az 1. ábrán láttunk erre példát). Az egyes megvalósításoknak tehát ezt az ideálisan biztonságos protokollt kell emulálniuk, olyan módon, hogy a kétféle végrehajtás (az ideális, illetve a valós) ne legyen algoritmikusan megkülönböztethető. Így jutottunk el az algoritmikus megkülönböztethetetlenségen alapuló szimulációs paradigmához: azt tekintjük biztonságosnak, ami az ideálistól algoritmikusan megkülönböztethetetlen. Egy picit formalizáltabb bemutatáshoz tekintsük a 3. ábrát, ahol a valós és az ideális rendszer sémája látható.

A komponensek a következők: futtató környezet (Z), a protokoll résztvevői (M1,…MN), a támadó (A, illetve S, a valós, illetve ideális rendszerben) valamint az ideális funkcionalitás (F). Az összekötések a kommunikációs kapcsolatokat jelzik. A 3. ábra szaggatott vonala az az interfész, amelyen keresztül Z futtató környezet látja az alatta futó rendszert (valóst vagy ideálisat), tehát Z a résztvevők outputját, valamint a támadó „közléseit” figyeli. A valós rendszerben láthatjuk a MIM-támadót, azaz a résztvevők közti minden kommunikáció rajta keresztül fut. Az ideális rendszer magja az F ideális funkcionalitás, a támadó csak ennek kontrollján keresztül interferálhat az ideális protokoll futásával. Ezek után a konstruált protokoll biztonságossága azt követeli, hogy Z környezet ne tudja megkülönböztetni, hogy az ideális vagy a valós rendszer fut-e alatta. Kissé formalizáltabban:

Pénzfeldobással sorsoljuk ki, hogy a valós vagy az ideális rendszert futtatjuk-e, amely sorsolás eredményéről Z nem tud. Ezután Z környezet kezdje futtatni a kisorsolt rendszert (a protokoll szerinti inputot adva résztvevőknek, illetve a támadónak is adhat induló információt, például a protokoll múltbeli futtatásaiból származó elemeket). Ekkor, ha tetszőleges valós támadó algoritmushoz (A) létezik olyan ideális támadó algoritmus (S szimulátor), hogy semmilyen Z algoritmus nem tudja megkülönböztetni, hogy melyik rendszert futtatja, a realizációt biztonságosnak tekintjük. Az így definiált biztonságosság mögötti intuíció az, hogy a valós támadó minden támadási „sikere” megkülönböztethetetlenül előállítható az ideális rendszerben is, márpedig ezen utóbbi rendszerben az ideális funkcionalitás definíciója szerint nem lehet sikeres.

A biztonság bizonyítás nem más, mint az S szimulátor algoritmusának a definiálása és annak megmutatása, hogy az sikeresen lefut, azaz bármit is próbál ügyeskedni a valós támadó, azt S utánozni képes az ideális rendszerben. Következésképpen, a kriptográfia ezen területén az alkalmazás feladatok is tétel-bizonyítás alapúak.

Sejthető, hogy az erős támadhatatlansági garanciák, amelyeket az univerzális komponálhatóság is nyújt, nincsenek „ingyen”. A mindennapi racionalitás, hogy ami nagyon jó, általában drága is. Az UC-biztonságosság erős garanciái sincsenek ingyen, ahol a költséget a megnövekedett számítási komplexitás jelenti. Jelenleg még lassúak a kapcsolatos realizációk. Ne felejtsük el, hogy egy gyakorlati feladatnál egy realizáció kapcsán mérlegre kell tenni a garanciák ereje mellett a futási sebességet is. Ezért áll elő ma még legtöbbször a helyzet, hogy egy alkalmazás „eladhatóságának” hatékonyságkényszere kompromisszumra készteti a tervezőt, és végül is az informális igazolási hátterű, de elegendő sebességű realizációt választja, elfogadható kis valószínűségű kockázatnak tekintve azt, hogy esetleg mégiscsak megtörésre kerül a konstrukció. Éppen ezért, a bizonyításos tervezési módszertanok (így az UC-módszertan) számára az egyik legfontosabb kutatási irány az algoritmikus komplexitás csökkentése (lásd például Lindell, 2011).

Végül is, konkrétabban mi az oka a bizonyított biztonságú kriptográfiai elemek (primitívek, protokollok) nagy algoritmikus komplexitásának? A probléma gyökere ott van, hogy a kapcsolatos egyirányú függvényeink még az inputról outputra történő számítás algoritmikus komplexitási osztálya szerint hatékony (PPT) végrehajtása is sok számítást igényel a biztonságosnak tekintett dimenziók mellett. Nem csoda, hogy ez az a pont, amelyen keresztül a kutatók a konstrukciók komplexitásából szeretnének lefaragni. Analóg komplexitáscsökkentés (sebességnövelés) volt a mozgatórugó az elliptikus görbék segítségével generálható algebrai struktúrákra épített kriptográfiai primitíveknél jó egy évtizeddel ezelőtt. Megjelennek nem standard, újabb keletű, nehéznek vélt feladatokra épített konstrukciók, amelyek jól hangzó komplexitásjavulást hirdetnek, ugyanakkor óvatosnak kell lennünk, mivel még nem eléggé analizáltak a kapcsolatos nehézségfeltételezések. Hétköznapi analógiával élve, a „fürge páncélozott autó” nehezen megvalósítható. Egy lehetséges természetes kompromisszum jelenleg ott jöhet létre, hogy erős, de költséges megoldásokat elsősorban ott alkalmazzunk, ahol valóban nagy a kockáztatott „érték”, és az nem a gyors, tömeges biztonsági szolgáltatások kategóriája. Nos, ha ez a helyzet, mi a gyakorlati jelentősége (haszna) jelenleg a bizonyított biztonságú konstrukcióknak, például az UC-módszertannak?

Általános alapvetésként az, hogy lehetséges biztonság garanciát adni igen erős támadói környezetben, anélkül, hogy bármilyen konkrét feltételezéssel élnénk a támadó PPT-algoritmus vonatkozásában. További sajátos és izgalmas ereje a módszertannak, hogy ebben realizálhatósági (egzisztencia), valamint nemrealizálhatósági tételek is bizonyíthatók tetszőleges kriptográfiai feladatra vonatkozó általánossággal. Egy nemrealizálhatósági tétel tipikus állítása arra vonatkozik, hogy bizonyos feltételek hiányában garantált biztonságigénnyel nem realizálhatunk kriptográfiai feladatokat. Ilyen feltétel lehet például egy harmadik megbízható fél elérhetősége (például publikus kulcsú infrastruktúra – PKI) vagy a protokoll résztvevői közti előzetes egyeztetés szükségessége. Maga a módszertan egy tervezési útmutató. Pragmatikus példaként tegyük fel, hogy megtervezünk egy protokollt bizonyított garanciákkal, azonban egy, a bizonyítás szerint alkalmazandó kriptográfiai primitív (például egy rejtjelező transzformáció) túl lassú, s ezt a primitívet helyettesítjük a „világon” legbiztonságosabbnak tartott, gyors, de ad hoc tervezésű (azaz nem bizonyított) primitívvel. Ekkor ugyan nem hivatkozhatunk a biztonság bizonyításunkra, de azt várhatjuk, hogy amíg a gyors primitív tartja a biztonsági tulajdonságait, a teljes protokollunk is biztonságos lesz. A gyakorlati hasznok közé sorolhatjuk egy felmerülő kriptográfiai feladat ideális funkcionalitás alapú definiálását, amelyre a módszertan számos példát ad. Helyszűke miatt nem taglalunk további gyakorlati előnyöket.

Reményeink szerint sikerült átadni az olvasónak valamennyi maradandót abból az izgalmas világból, amelyet modern kriptográfiának hívnak. Ez a terület az egyik legszebb példája annak, amikor addig külön fejlődő tudományterületek szintézise gyors fejlődést, mélyebbre hatolást hoz. A modern kriptográfia a klasszikus információelméleti/algebrai megközelítésekkel sikeresen ötvözi a számítástudomány korszerű módszereit.
 

Kulcsszavak: bizonyított biztonság, protokollanalízis, algoritmikus megkülönböztethetetlenség, szimulációs paradigma, univerzális kompozíció
 

IRODALOM

Blum, Manuel (1981): Coin Flipping by Telephone. CRYPTO. 1981, 11–15. • WEBCÍM

Blum, Manuel - Micali, Silvio (1984): How to Generate Cryptographically Strong Pseudo-random Bits. SIAM Journal of Computing. 13, 4, 850–863. • WEBCÍM

Canetti, Ran (2000): Universally Composable Security: A New Paradigm for Cryptographic Protocols. Cryptology ePrint Archive: Report 2000/067 • WEBCÍM

Goldreich, Oded (2007): Foundations of Cryptography, Vol. 1–2. Cambridge Univ. Press, Cambridge Vol 1: • WEBCÍM Vol 2: • WEBCÍM

Goldreich, Oded – Micali, S. – Wigderson, A. (1987): How to Play ANY Mental Game. In: Proceedings of the 19th Annual ACM Conference on Theory of Computing. ACM Press, 218–229. • WEBCÍM  

Lindell, Yehuda (2011): Highly-Efficient Universally-Composable Commitments Based on the DDH Assumption. EUROCRYPT 2011 • WEBCÍM

Pfitzmann, Birgit – Waidner, Michael (2000): Composition and Integrity Preservation os Secure Reactive Systems. In: Proceedings of the 7th Conference on Computer and Communication Security of the ACM. 245–254.

Vajda István (2013a): A Universal Composability Framework for Anonymous Communications. Journal of Computer and Communications Security. 3, 3, 33–44.

Vajda István (2013b): Provably Secure On-demand Routing Protocols. Pioneer Journal of Computer Science and Engineering Technology, 6, 1–2, 19–39.

Vajda István (2014): A Proof Technique for Security Assessment of On-demand Ad Hoc Routing Protocols. International Journal of Security and Networks, 9, 1, 12–19.  DOI: 10.1504/IJSN.2014.059329

Vajda István (2015a): Can Universally Composable Cryptographic Protocols Be Practical? International Journal of Computer Network and Information Security. 7, 10, 1–12. DOI: 10.5815/ijcnis.2015.10.03

Vajda István (2015b): On the Analysis of Time Aware Protocols in Universally Composable Framework. International Journal of Information Security. 14, 4, 1–10. DOI: 10.1007/s10207-015-0300-2

Yao, Andrew C. (1982): Protocols for Secure Computations. In: Proceedings of the 23rd Annual Symposium on Foundations of Computer. IEEE Computer Society Washington, 160–164. DOI: 10.1109/SFCS.1982.88 • WEBCÍM

LÁBJEGYZETEK

1 A kriptográfiai primitív egy általánosan használt építőelem (például rejtjelező transzformáció vagy digitális aláírás), míg a kriptográfiai protokoll két vagy több résztvevő közti biztonságos párbeszéd valamely biztonsági feladat közös végrehajtására. A protokollok a primitíveket építőelemként használják. <

2 Modulo 2 a 2-vel való osztás maradéka. <

3 Az XOR „kizáró vagy” logikai művelet, amelyik nem engedi meg, hogy a két állítás logikai értéke egyszerre igaz legyen. <