A modern tudomány kialakulásához vezető folyamatban, az ún. tudományos forradalomban meghatározó szerepet játszott a 16. századi lengyel-porosz tudós, Nicolaus Kopernikusz csillagászati hipotézise. A hipotézis szerint az égitestek mozgásának középpontjában nem a Föld áll, mint ahogy azt a korábbi csillagászati hagyomány uralkodó elképzelései vallották, hanem a Nap – ezért Kopernikusz hipotézisét heliocentrikusnak nevezik. Ez az elképzelés döntően befolyásolta a tudományok későbbi fejlődését, ugyanis olyan elméletek kidolgozását ösztönözte (Johannes Kepler bolygómozgás-törvényeitől Giordano Bruno kozmológiáján és Galileo Galilei mechanikáján keresztül Isaac Newton fizikájáig), amelyek alapvetően meghatározták a modern tudomány arculatát. Mi sem mutatja jobban ezt a hatást, mint az, hogy a tudományos forradalmat sokan éppen az 1543-as évtől, Kopernikusz nagy csillagászati munkájának, a De revolutionibus orbium coelestium-nak (Az égi pályák forgásáról) a megjelenésétől datálják (lásd például a Wikipedia angol és magyar nyelvű vonatkozó szócikkeit).

Ugyanakkor ez a forradalmi elgondolás csak lassan, generációkkal Kopernikusz után vált általánosan elfogadottá. Ebben nemcsak az játszott szerepet, hogy a napközéppontú csillagászat elfogadása szükségessé tette a fizika alapfogalmainak újragondolását (hiszen az arisztotelészi–középkori fizika számos elve a földközéppontú hipotézisre épült), hanem az is, hogy Kopernikusz elképzelésének helyességére igen nehéz volt bizonyítékokat találni. A Föld Nap körüli keringésére adott empirikus bizonyítékok csak 1838 után, a közeli csillagok ún. éves parallaxisának kimérésével váltak elérhetővé, míg a Föld forgását először Léon Foucault híres ingakísérletével igazolták 1851-ben. Mégis, nagyjából a 17. század derekától, mintegy száz évvel Kopernikusz halálát követően általánosan elfogadottá váltak a kopernikuszi tanok, pontosabban azoknak a Kepler, majd Newton és mások által módosított változatai, annak ellenére, hogy az empirikus bizonyítékokra még nagyjából további kétszáz évet kellett várni. Jogos tehát Kopernikusz elméletét „hipotézisnek” nevezni, és nem csak a szónak abban az eredeti értelmében, amelynek megfelelően Kopernikusz korában minden, a bolygómozgásokat leíró matematikai elméletet hipotézisnek neveztek.

Felmerül tehát a kérdés, hogy mi késztette a modern tudomány úttörőit arra, hogy bizonyítékok híján is elfogadják Kopernikusz hipotézisét. A válasz szinte reménytelenül összetett, és Galilei távcsöves megfigyeléseitől Kepler rendkívül pontos előrejelzésein át Newton mozgástörvényeiig rengeteg tényezőt magában foglal. Ebben az írásban egy ennél szűkebb kérdésre keresem a választ: mik voltak a kopernikuszi hipotézis mellett szóló első érvek – azok, amelyek hatására a kezdeti támogatók (Kepler, Galilei) szembefordultak a görög eredetű csillagászati tradíció kétezer éves földközéppontú örökségével? Melyek azok az érvek, amelyekre maga Kopernikusz támaszkodott?

Mielőtt rátérek a válasz körvonalazására, érdemes néhány előzetes negatív megjegyzést tenni, és kiemelni, hogy a népszerű összefoglalások állításaival szemben mik nem voltak jellemzők Kopernikusz hipotézisére. Azt állítom, hogy bár Kopernikusz műve forradalmi hatást váltott ki, maga a mű számos szempontból nem volt forradalmi munka (lásd például Kuhn, 1985, 134–136.). Először is, Kopernikusz rendszere nem pontosabb, mint ókori „riválisáé”, az i. sz. 2. századi Klaudiosz Ptolemaioszé, akinek Nagy matematikai összefoglalása (Almageszt) a technikai csillagászat alapkönyvének számított a 16. században is. Bár kétségtelen, hogy a Kopernikusz műve alapján készült Porosz táblázatok (1551) többnyire pontosabb előrejelzéseket tettek, mint a korábban leginkább elterjedt, a 13. században összeállított Alfonz-féle táblázatok, ám ez elsősorban az újabb megfigyeléseknek és az ezeken alapuló számításoknak volt betudható. Kopernikusz rendszere elviekben nem írja le pontosabban a bolygómozgásokat Ptolemaioszénál, hiszen nagyjából ugyanazokat a (Kepler nyomán tévesnek bizonyult) matematikai szerkesztési elveket használja, mint a görög csillagász. A pontosságbeli forradalmat Kepler törvényei indítják majd el, amelyek Kopernikusztól távol álló elveken alapulnak.
Ez összefügg a második negatív állítással: Kopernikusz rendszere nem modernebb, mint Ptolemaioszé. Hiszen ugyanazokat a modellezési technikákat alkalmazza, mint Ptolemaiosz: az excentereket és az epiciklusokat (1. ábra). Igaz ugyan, hogy Kopernikusz elveti Ptolemaiosz módszerének harmadik elemét, az ekvánspontot, ám ebben korántsem modern szempontok vezérlik, ugyanis azért nem fogadja el azt, mert alkalmazása sérti a platóni elvet, az egyenletes körmozgások követelményét, amihez Kopernikusz ugyanannyira ragaszkodik, mint az őt megelőző kétezer éves csillagászati tradíció egésze (és amit éppen Kepler nyomán fognak száműzni a csillagászatból). Másrészt Kopernikusz gyakorlatilag változtatás nélkül megismétli az Almageszt matematikai megalapozását, vagyis a trigonometria elveinek geometriai keretben történő felépítését, figyelmen kívül hagyva azokat az egyébként általa jórészt ismert innovációkat, amelyeket iszlám és európai matematikusok bevezettek a Ptolemaiosz ideje óta eltelt másfél évezred során.

A modernség hiánya a kozmológiai elképzelésekben is tetten érhető. Mint ahogy elődei, Kopernikusz is fenntartások nélkül beszél az égitesteket hordozó szférákról, bár ezek természetét ő sem tárgyalja, hiszen ez – Arisztotelész elképzelése szerint – nem a matematikai csillagászat feladata. Ugyanebből az okból a bolygómozgások okának kérdését sem firtatja, ugyanis a csillagász hagyományosan elfogadott szerepe pusztán abban áll, hogy matematikai modellt szerkesszen az égitestek mozgásához, és Kopernikusz teljesen elfogadja ezt a szerepet. Amennyi fizikára egyáltalán utal a műve bevezető jellegű fejezeteiben, az teljesen arisztoteliánus természetű. Érthető kivétel ez alól a nehézkedés, vagyis gravitatio fogalma, amely szerinte „nem más, mint egyfajta természetes vágy, melyet a mindenség Teremtője helyezett a dolgok részeibe, hogy azok egymáshoz tapadjanak, és gömb alakjában egyesüljenek” (Kopernikusz, 1543, 7.) (ugyanis az arisztotelészi magyarázat, hogy a nehéz testek a világ középpontja felé törekednek, nem működik akkor, ha nem a Föld van a világ közepén). Végül fontos megjegyezni, hogy Kopernikusz ugyanúgy egy véges, gömb alakú és a csillagok szférája által határolt világegyetemet ír le, mint Ptolemaiosz, ami mellett éppen a mű legelső fejezetében érvel.

Harmadjára le kell szögezni, hogy Kopernikusz elmélete korántsem egyszerűbb, mint Ptolemaioszé. Az epiciklusok és excenterek használata miatt ugyanis az égitestek pályája bonyolult szerkesztéseket igényel, és a pályák összessége körülbelül ugyanannyi körből állítható össze, mint Ptolemaiosz világa. Arról nem is beszélve, hogy míg a földközéppontú hipotézis alapján az égitestek látszó pozíciói közvetlenül számíthatók a pályakörökből (hiszen a megfigyelő azok középpontjában áll), addig a napközéppontú rendszerben mind a Föld, mind a kérdéses égitest pozícióját külön-külön ki kell számítani ahhoz, hogy az égi pozíció előre jelezhető legyen, és ennek megfelelően a kopernikuszi modell számításai jóval bonyolultabbak gyakorlati szempontból, mint a ptolemaiosziak.

Persze maga Kopernikusz – a ma elterjedt sztereotípiák ellenére – nem is állítja azt, hogy modellje pontosabb vagy modernebb volna, mint Ptolemaioszé (bár időnként egyszerűbbnek feltételezi, ám ez az egyszerűség nem a matematikai részletekből adódik, hanem azokból az összefüggésekből, amelyeket alább tárgyalok). Ha meg akarjuk érteni, miben látta hipotézisének előnyeit, kénytelenek vagyunk magukhoz a fennmaradt szövegekhez fordulni. Ám ezen a ponton egy súlyos problémába ütközünk: nem sok szöveg maradt fenn tőle. Szemben számos reneszánsz és koramodern tudóssal, Kopernikusztól nem maradt ránk például terjedelmes levelezés, amely alapján belepillanthatnánk személyesebb motivációiba, vagy viták kontextusában láthatnánk az érveit, és nem állnak rendelkezésre olyan, korai munkák sem, amelyekben kifejlődésében vizsgálhatnánk a napközéppontú hipotézist.

Három csillagászati munkájáról tudunk. Az első egy rövid, kéziratos mű, amelyet soha nem szánt kiadásra, a Kis kommentár az égi mozgások hipotéziséhez (röviden Commentariolus-ként szokás hivatkozni rá). Hogy pontosan mikor írta, azt ma már lehetetlen megállapítani, az első említése 1514-ből származik, bár feltehetőleg néhány évvel korábban keletkezett. A második egy ennél is rövidebb, felkérésre írt levél 1524-ből, amelyben egy kortárs csillagász, Johannes Werner munkáját kritizálja – ez szintén nem megjelenésre szánt szöveg. A harmadik pedig maga a De revolutionibus, amelyen ugyan évtizedeken át dolgozott, de csak halálának évében, 1543-ban jelentette meg, környezete hosszas unszolására. Mivel a Werner ellen írt levele nem utal Kopernikusz saját modelljére, a heliocentrikus hipotézisre, ezért csak a Commentariolus és a De revolutionibus szolgálhat e tanulmány alapkérdése számára elsődleges forrásul.

A Commentariolus felvázolja a napközéppontú hipotézis alapjait. Ebben a rövid ismertetésben Kopernikusznak szemmel láthatólag nem az a célja, hogy hosszasan érveljen alapelvei mellett, vagy, hogy alaposan ismertesse modelljének matematikai részleteit (amelyek feltehetőleg még nem is álltak teljesen készen). Az alapelvek tömör felsorolása után körvonalazza rendszerének főbb elemeit, vagyis hogy az egyes égitestek mozgását hány kör segítségével és azok milyen elrendezésével tudja visszaadni. Bár bizonyos részletek eltérnek még a De revolutionibus rendszerétől, de az alapvető elemeiben megegyezik vele.

De vajon miért van szükség a napközéppontú hipotézisre? A mű bevezetője röviden ismerteti a korábbi csillagászati rendszerek elveit, majd kijelenti, hogy talán kigondolható „a körök egy ésszerűbb elrendezése, amelyből minden látszó egyenlőtlenség levezethető, és amelyben minden a saját központja körül mozog egyenletesen, ahogy azt az abszolút mozgás szabálya megkívánja” (Kopernikusz, 1971, 57.). Ezek után lefekteti saját feltevéseit, majd kijelenti: „Ezen feltevések leszögezése után megpróbálom megmutatni, hogy miként lehet módszeresen megőrizni a mozgások egyformaságát.” (Kopernikusz, 1971, 59.) Tehát úgy tűnik, hogy a korábbi hipotézisek problémája az „egyformaság” és a közös rendező elv hiánya. De vajon mi lehet az a rendező elv, amelyből a rendszer részletei levezethetők? Ez kiderül a feltevésekből:

„1. Az égitesteknek és égi szféráknak nincs egyetlen központjuk.

2. A Föld központja nem központja az univerzumnak, hanem csak a gravitációnak és a Hold szférájának.

3. Minden szféra a Nap mint középpont körül mozog, így a Nap az univerzum központja.

4. A Föld–Nap-távolság aránya a csillagos ég magasságához olyan sokkal kisebb, mint a Föld sugarának aránya a Naptól mért távolságához, hogy a Föld–Nap-távolság észrevehetetlenül kicsi a csillagos ég magasságához képest.

5. A csillagos ég mozgásának látszata nem a csillagos ég valódi mozgásának, hanem a Föld mozgásának következménye. A Föld a környező elemekkel együtt naponta egyszer megfordul rögzített pólusai körül, míg a csillagos és a legfelsőbb mennyek mozdulatlanul maradnak.

6. A Nap mozgásának látszata nem saját mozgásának, hanem a Föld mozgásának következménye, mellyel ugyanúgy keringünk a Nap körül, mint bármelyik másik bolygó. Így a Földnek egynél több mozgása is van.

7. A bolygók látszó retrográd és direkt mozgásai nem saját mozgásuknak, hanem a Föld mozgásának következményei. A Föld mozgása tehát képes magyarázatot adni az egek mozgásában látszó számos egyenlőtlenségre.” (Kopernikusz, 1971, 58-59., kiemelés tőlem)

Egyfelől azért idéztem a feltevéseket teljes terjedelmükben, mert semmilyen más szövegében, tehát a De revolutionibus vonatkozó fejezeteiben sem fejti ki ennyire tömören és világosan a heliocentrikus rendszer alapjait. Másrészt az általam kiemelt szövegrészekben tetten érhető az a közös rendező elv, amelyet keresünk: ez nem más, mint a Föld mozgása, amely magyarázatot ad a mozgások rendszerének számos elemére.

Ugyanez a téma megjelenik a De revolutionibus-ban is. Ennek Előszavában, amelyet III. Pál pápához ajánl, hosszasabban kritizálja az ókori elméleteket. Szemükre hányja: „Arra sem voltak képesek, hogy felfedezzék vagy levezessék a legfontosabb belátást, vagyis az univerzum szerkezetét és részeinek valódi szimmetriáját. Ellenben pontosan úgy jártak el, mint aki különböző helyekről vesz kezeket, lábakat, fejet és más részeket, amelyek gyönyörűen vannak ugyan megformálva, de nem ugyanahhoz a testhez tartoznak, és így nem felelnek meg egymásnak – az ilyenekből inkább egy szörnyet, semmint embert lehet összeállítani.” (Kopernikusz, 1543, iv)

Ez a passzus tehát ismét csak arra utal, hogy a földközéppontú rendszerek képtelenek egységesen, közös rendező elv alapján tárgyalni a részleteket. Különösen árulkodó a „szimmetria” kifejezés és az erre épülő művészeti metafora (részletes elemzésért lásd: Hallyn, 1990). Bár a szimmetria szó eredeti értelmében összemérhetőséget jelent (ez nagyjából a matematikai mennyiségek racionális voltának felel meg), az a jelentés, amit Kopernikusz és kora tulajdonít neki, az i. e. 1. századi építésztől, Marcus Vitruviustól származik: „A szimmetria egy mű részeinek megfelelő elrendezése, valamint a részeknek és általában az egésznek a viszonya, egy bizonyos részhez mint mércéhez képest. Így például az emberi testben egyfajta szimmetrikus harmónia áll fenn az alkar, a láb, a tenyér, az ujj és egyéb kis részek között; és ugyanez a helyzet a tökéletes épületekkel is.” (Vitruvius, 1955, 27.)

Vitruvius tehát ugyanazt a metaforát használja, mint Kopernikusz: az emberi testrészek közti megfelelést. Ez a fajta szimmetria rendkívül fontos elv volt a reneszánsz képzőművészetben: ezt illusztrálta Leonardo da Vinci híres rajzával, a Vitruvius-tanulmánnyal (2. ábra), amelynek magyarázatában azt írja le, milyen számok szerint aránylanak az egyes testrészek egymáshoz, valamint erről szól Albrecht Dürer Négy könyv az emberi arányokról című műve is. A szörny fogalma nem azt jelentette, mint ma (vagyis egyfajta ijesztő, emberre veszélyes természetfeletti vagy mesebeli lényt), hanem olyan lényt, amely nem egymásnak megfelelő részekből, torzan állt össze.

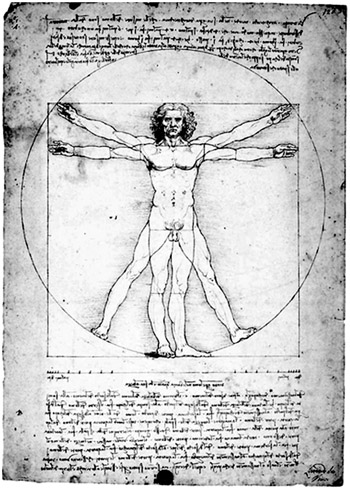
2. ábra • Leonardo Vitruvius-tanulmánya

Ha alaposabban meg akarjuk érteni a metafora csillagászati értelmét, akkor előre kell lapoznunk Kopernikusz művében az Első könyv 10. fejezetéhez (Az égi pályák rendje), ahol Kopernikusz leírja az égitestek sorrendjét kívülről, az állócsillagok szférájától befelé, a középponti Nap felé haladva, majd ezzel foglalja össze rendszerét: „A rendezettség mögött tehát a kozmosz csodálatos szimmetriája rejtőzik. Tiszta harmónia uralkodik a szférák mozgásában és méretében, amely másképpen fel sem fogható. Így ugyanis érthetjük, miért nagyobb a Jupiter progressziója és retrogressziója, mint a Szaturnuszé, ám kisebb, mint a Marsé […], valamint azt is látjuk, hogy az ilyen oszcillációk miért gyakoribbak a Szaturnusznál, mint a Jupiternél […] továbbá, hogy a Szaturnusz, a Jupiter és a Mars miért vannak közelebb a Földhöz, amikor oppozícióban állnak a Nappal, mint amikor elvesznek a Nap sugarai közt, s majd újra előbukkannak onnan. […] Mindezen jelenségek ugyanazon okból következnek, vagyis a Föld mozgásából.” (Kopernikusz, 1543, 10.)

Lássuk az egyes elemeket sorjában!

A bolygók „progressziója és retrogressziója” arra a jelenségre utal, hogy bár a megfigyelés szerint a bolygók a Naphoz és a Holdhoz hasonlóan egy adott irányban és nagyjából egy közös kör (az ekliptika) mentén, a rájuk jellemző periódussal körben haladnak (progresszió) – mármint az állócsillagok háttere előtt, vagyis ha leszámítjuk az égbolt minden égitestre közös napi körülfordulását –ám szabályos, saját pályájukra jellemző időközönként megtorpannak, és rövidebb ideig visszafelé haladni látszanak (retrogresszió). Ezt a „hurkos” mozgást adja vissza Ptolemaiosz az epiciklusok segítségével, hiszen, ha megfelelően választjuk a körök méreteit és a rájuk jellemző keringési időket, akkor a két forgás eredője valóban hurkokat ír le, így a középponti Földről nézve a bolygók haladását hátráló szakaszok szakítják meg. Ugyanakkor Ptolemaiosz rendszerében fel sem merül az a kérdés, hogy miért éppen akkorák a hátráló szakaszok, vagyis mi határozza meg az epiciklus-körök méretét: ez egyszerűen a megfigyelésekből következik, és a jelenségekhez illesztjük a modell paramétereit.

Kopernikusznál viszont ez utóbbi kérdés új értelmet nyer. Az ő hipotézise szerint – ahogy a Commentariolus imént idézett 7. feltevésében le is szögezi – a hátráló mozgás nem valódi, hanem csak látszólagos, annak következménye, hogy a megfigyelő nem a középpontban áll nyugalomban, hanem a középpont körül kering. Amikor a Föld belülről „leelőz” egy külső bolygót (vagy amikor egy belső bolygó belülről „leelőzi” a Földet), akkor a mozgó Földről nézve úgy látjuk, mintha a megfigyelt bolygó visszafelé haladna egy ideig az állócsillagok hátterén, hasonlóan ahhoz, mint amikor egy gyorsabb járműben ülve úgy látjuk, mintha a lassabb, éppen leelőzött jármű hátrálna a háttérhez képest, pedig valójában előre halad. Hogy a Jupiter hátrálása nagyobb, mint a Szaturnuszé, az azzal magyarázható, hogy a Jupiter közelebb van a Földhöz, így a Föld keringéséből származó látszólagos hurok nagyobb lesz a csillagszférára vetítve, mint a távolabbi Szaturnusz látszólagos hurka (3. ábra). És természetesen a többi bolygó viszonylatában is pontos, számszerű értelmet nyer minden ilyen összehasonlítás.

Ugyanígy magyarázható a második állítás is, amely a visszafordulások gyakoriságára vonatkozik. Ptolemaiosz rendszerében ez is csak fenomenologikus paraméter, amelyet a megfigyelt jelenségekhez illesztünk. Kopernikusz azonban erre is képes mélyebb magyarázatot nyújtani: mivel a keringő Föld gyakrabban éri utol és előzi le a Szaturnuszt, mint a gyorsabban és kisebb pályán keringő Jupitert, így ebből következik, hogy a Szaturnusz esetén gyakrabban figyelhetjük meg az oszcillációkat, mint a Jupiternél (4. ábra) – pontosan a keringési idők viszonyai szerint.

A harmadik állítás a bolygók fényességváltozásaira vonatkozik. Kopernikusz rendszerében világos (5. ábra), hogy egy külső bolygó akkor van legközelebb a Földhöz, tehát akkor tűnik legfényesebbnek, amikor oppozícióban áll a Nappal (vagyis az égbolt átellenes pontjain helyezkednek el). A fényességváltozásokra és ezek szélső értékeire Ptolemaiosz epiciklusai is magyarázatot adnak, igaz, nem olyan pontosan, mint a kopernikuszi rendszer, viszont arra nem, hogy ezek milyen összefüggésben állnak a Nap mozgásával. Kopernikusz rendszeréből fény derül erre is: valójában nem a Nap, hanem a Föld mozgásával függnek össze, mert elsődlegesen ez határozza meg a bolygók tőlünk mért távolságát, nem pedig az epiciklusok. (A technikai részletek megértéséhez további segítség a Bolygómozgás régen és ma [URL1] címen elérhető animáció.)

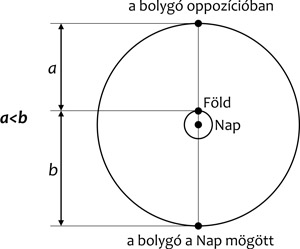
5. ábra • A Szaturnusz, a Jupiter és a Mars miért vannak közelebb a Földhöz, amikor oppozícióban állnak a Nappal, mint amikor elvesznek a Nap sugarai közt? (Lásd a szöveget.)

Összefoglalva tehát azt láthatjuk, hogy a kopernikuszi hipotézis összefüggést teremt számos olyan megfigyelhető jelenség között, amelyek a földközéppontú elméletben csak független, közvetlenül a megfigyelések által diktált elemek voltak. Ennyiben azt is mondhatjuk, hogy a kopernikuszi hipotézis egy magyarázati rendszerré áll össze, és ennek a rendszernek a közös magyarázó elvét, azaz a közös „mértékét” (lásd Vitruvius meghatározását) a Föld mozgása adja. Ugyanezt emeli ki Georg Joachim Rheticus, Kopernikusz egyetlen tanítványa és munkatársa, aki 1539-ben érkezett az idős csillagászhoz, hogy rávegye a vonakodó mestert várva várt művének kiadására. Miközben Kopernikusz sajtó alá rendezte a kéziratokat, Rheticus írt egy gyors összefoglalást a nagy műről, hogy minél hamarabb tájékoztassa, egyben felkészítse a közönséget a várható elmélettel kapcsolatban. Az 1540-ben megjelent Első összefoglalás (Narratio Prima) népszerű és könnyen, matematikai ismeretek nélkül is áttekinthető ismertetést nyújt a heliocentrikus hipotézisről. A hosszas és óvatos bevezető fejezetek, a lehetséges ellenérvek tompítása után végül Rheticus előrukkol a napközéppontúság gondolatával, és méltatja a rendszer szimmetriájának előnyeit: a bolygómozgások „közös mértéke az a nagy kör, amely a Földet szállítja, mint ahogy a gömb alakú Föld sugara közös mértéke a Hold körének, a Hold és a Nap távolságának stb.” (Kopernikusz, 1971, 147.)

Azt, hogy a bolygómozgásokban van közös mérték, már korábban is lehetett sejteni, és erre utaltak a 15. században újjáéledő matematikai csillagászati hagyomány úttörői, Georg von Peurbach és Regiomontanus (Johannes Müller) is. Bár Ptolemaiosz az Almagesztben külön-külön, egymástól függetlenül tárgyalja az égitestek mozgását, és nem kísérli meg ezeket egyetlen rendszerré összefogni, ám a pályák összevetésével különös egybeesések fedezhetők fel a bolygók és a Nap mozgásai között. Kiderül ugyanis, hogy a „belső” bolygók (Merkúr és Vénusz) esetén az epiciklus-kör középpontja mindig a Nap irányába mutat, valamint hogy a „külső” bolygók esetén (Mars, Jupiter, Szaturnusz) az epiciklus-kör középpontját és a bolygót összekötő sugár mindig párhuzamos a Naptól a Föld irányába mutató egyenessel. (Ez utóbbi összefügg a fényességváltozások és a Nap helyzete közti, fent említett megfeleléssel.) Megalapozott volt tehát a sejtés, hogy a Nap szerepe kitüntetett a mozgások rendszerként tekintett összességében. Kopernikusz hipotéziséből azonban kiderül, hogy a Nap közös elemként jelentkező mozgása valójában csak látszólagos, és a Föld Nap körüli mozgása az, ami mértékként szolgál. Ez a keringés jelenik meg a belső bolygók deferens (vagyis az epiciklust hordozó nagyobb kör) menti mozgásában és a külső bolygók epiciklus-mozgásában. Egy látszólagos mozgáskomponens, amely egyszerre van jelen szinte minden égi mozgásjelenségben – kivéve az állócsillagokat, amelyeket éppen ennek hiánya miatt gyakorlatilag végtelenül távolinak kell tekintenünk, illetve a Holdat, amely a Földdel együtt végzi keringését a Nap körül.
A kopernikuszi hipotézis fő előnye tehát az, hogy egységes magyarázati rendszert nyújt az égi mozgásjelenségek többségére. Ahhoz azonban, hogy a De revolutionibus olvasója felfoghassa ezt az előnyt, meg kell értenie a rendszer egészét, és el kell mélyednie a részletekben. Nem lehetséges tehát döntő, bizonyító erejű érvet szolgáltatni a mű elején, ami azonnal eloszlatná a kétségeket. Ezt jól tudta Kopernikusz is, amikor ezt írta az Első könyv 5. fejezetében (Végez-e mozgást a Föld, és mi a helye?): „Mert ha valaki tagadja, hogy a Föld a világ közepén vagy centrumában van, ugyanakkor nem ismeri el, hogy kettejük távolsága elég nagy ahhoz, hogy mérhető legyen az állócsillagok távolságához, mégis úgy gondolja, hogy e távolság láthatóan nagy a Nap és a bolygók pályaköreinek viszonylatában, és ha ezek után azt gondolja, hogy a testek mozgása azért tűnik szabálytalannak, mert más középpont körül vannak elrendezve, mint a Föld középpontja, akkor talán képessé válik arra, hogy előhozakodjon egy tökéletesen elfogadható magyarázattal a szabálytalannak látszó mozgásra.” (Kopernikusz, 1543, 3.)

Világos, hogy a rendszer előnyének megértéséhez egy sor olyan, előzetes hipotézist kell elfogadunk, amely ellentmond a hagyományos elképzeléseknek. Fel kell tennünk, hogy a Föld nem a világ középpontjában áll, hanem abból kimozdítva mozog (ez utóbbi az elemi hétköznapi tapasztalattal is ellentétben áll). De azt is fel kell tennünk, hogy kimozdítottságának mértéke elhanyagolható a világ méretéhez képest – tehát a világ sokkal nagyobb, mint korábban gondolták. Hiszen míg a földközéppontú hipotézis szerint a Nap valahol a világ peremén vagy annak közelében mozog, így a világ mérete durván megfelel a Nap–Föld-távolságnak, addig Kopernikusz szerint ez utóbbi távolság elhanyagolhatóan kicsi a világ határát alkotó állócsillagok távolságához képest (lásd a Commentariolus 4. feltevésében kifejtett aránypárt). De azt is fel kell tételeznünk, hogy a bolygók pályakörei összemérhetők a Föld körének méretével – vagyis azok sem a csillagok közelében, hanem annál sokkal-sokkal lejjebb keringenek. És végül fel kell tennünk, hogy a mozgásokat nem a megfigyelő felől, hanem egy attól távoli pont (a Nap) felől tekintve kell értelmeznünk. És mindezzel nem azt nyerjük, hogy egyszerűbb vagy pontosabb leíráshoz jutunk a mozgásokról, hanem pusztán annyit kapunk, hogy felfedezünk bizonyos összefüggéseket, és magyarázatra lelünk egyes mozgáskomponensek viszonylatában.

Mégis, ez a nyereség nem csekély, ugyanis általa érthetőbbé válik a világ. Abban a korban, amikor elterjedt volt a nézet, hogy a világ szerkezete matematikai természetű harmóniákra épül, és hogy a Teremtő egy matematikában kifejezhető rend szerint tervezte a mindenséget, Kopernikusz elméletének elfogadása kifizetődőnek tűnhetett azok számára, akik a kellő kompetenciával rendelkeztek, és vették a fáradságot a megértéséhez. Közéjük tartozott Kepler és Galilei, akik átlátták Kopernikusz üzenetét, majd továbbfejlesztették azt, és másoknak is átadták, hogy ezzel utat nyissanak a tudomány gyökeres átalakulásának. Mi pedig, Kopernikusz örökségének birtokosaként, az évszázadok távlatából visszatekintve szinte nem is értjük, miért tarthatott ennyi ideig az emberiségnek, hogy kidolgozza és elfogadja ezt az alapvető igazságot: a Föld mozgásának tézisét. Ám látva a fenti gondolatmenet jellegét és nehézségeit, vessük fel a kérdést: ha mi négyszáz évvel ezelőtt élünk, vajon elég meggyőzőnek találtuk volna Kopernikusz érveit ahhoz, hogy beálljunk a követői közé?
 

Kulcsszavak: csillagászattörténet, heliocentrikus hipotézis, Kopernikusz, szimmetria, tudományos forradalom
 

IRODALOM

Hallyn, Fernand (1990): The Poetic Structure of the World. Copernicus and Kepler. Zone Books, New York

Kopernikusz: Copernicus, Nicolaus (1543): De Revolutionibus Orbium Coelestium. Petreius, Nürnberg • WEBCÍM

Kopernikusz: Copernicus, Nicolaus (1971): Three Copernican Treatises: the Commentariolus of Copernicus, the Letter against Werner, the Narratio prima of Rheticus. Edited and translated by Edward Rosen. Octagon Books, New York

Kuhn, Thomas S. (1985): The Copernican Revolution. Harvard University Press, Cambridge • WEBCÍM

Vitruvius, Marcus Pollio (1955): On Architecture. (ed. Granger, Frank) Harvard University Press, Cambridge

URL1: Bolygómozgás régen és ma • WEBCÍM