Bevezetés

A tudomány iránt érdeklődő olvasók minden bizonnyal sokat tudnak a nanotudomány és nanotechnológia csodálatos eredményeiről. A biotechnika, az elektronika, a számítástechnika és az anyagtudomány számos új vívmánya atomi méretű vagy annál nem sokkal nagyobb szerkezetekkel kapcsolatos. Viszonylag tág értelmezéssel, a nanotudomány olyan objektumok vizsgálatával foglalkozik, amelyek kiterjedése legalább egy irányban (dimenzióban) a néhány tized nanométer (1 nm = 10^-9 m) és az egy mikrométer (1 µm = 1000 nm) közötti mérettartományba esik. Figyelembe véve, hogy az átlagos atomi méret 0,2–0,3 nm, ez a definíció magában foglalja egy hordozóanyag belsejében vagy felületén abszorbeált individuális atomokat, valamint a több száz nm kiterjedésű, több tízmillió atomot tartalmazó nanokristályokat is. Napjaink tudományos-technológiai forradalmában játszott szerepe mellett a nanotudománynak az ad különleges jelentőséget, hogy ezen a méretskálán újszerű és meglepő jelenségek tapasztalhatók, amelyek megértése csupán a kvantummechanika törvényszerűségei alapján lehetséges. A nanotudományon belül a nanomágnesség önmagában is tág tudományterület. A cikk rövid betekintést nyújt a nanomágnesség témakörébe és eredményeibe. Természetesen nem próbálhatjuk meg a teljes témát felölelni, és az is valószínű, hogy ez az összefoglaló inkább egy elméleti kutató szemléletéhez áll közel.¹

Számos baktériumban, puhatestűben, rovarban és egyéb állatban találhatók mintegy 40–100 nm méretű magnetit (Fe₃O₄) nanorészecskék, amelyek mágneses szenzorként a Föld mágneses terét érzékelik. Hasonló részecskék vannak bizonyos kőzetekben és ásványokban (például mágnesvaskő). Ezek segítségével archeomágneses kormeghatározás végezhető, vagy a Föld mágneses terének hosszú időskálán történő változását lehet nyomon követni. A nanomágnesség túlnyomórészt mesterségesen előállított nanoanyagokkal foglalkozik. Ilyenek például a mágneses nanokompozitok, amelyek fémüvegekből állíthatók elő részleges átkristályosítással. Szerkezetükre jellemző, hogy 1–50 nm átmérőjű Fe-, illetve Fe-Si- nanorészecskék vannak beágyazva egy amorf hordozóanyagba. A szemcsék méretétől és összetételétől függően ezek a nanokompozitok lehetnek állandó mágnesek, lágy mágnesek vagy magnetorezisztív anyagok (lásd később). Az utóbbi évtizedekben számos módszerrel, amelyek leírására itt nem tudunk kitérni, a legkülönbözőbb méretű és alakú nanoszerkezeteket állították elő. A Ralph Skomski összefoglalójából kölcsönvett 1. ábrán (Skomski, 2003) a mesterségesen létrehozott nanoszerkezetek gyakori geometriai típusait mutatjuk be. Az új nanostruktúrák gyártásának motorja a funkcionálisan tökéletesebben működő, sok esetben teljesen új minőségű eszközök fejlesztése. A mágneses felületek, vékonyrétegek és multirétegek (rétegsorok) jól elkülönülő kutatási területet jelentenek a nanomágnességen belül. Ezek a rendszerek csak egy dimenzióban véges méretűek, és a felülettel párhuzamosan végtelennek tekinthetők, ezért sok jelenség itt érthető meg, illetve tanulmányozható legjobban.

Mágneses kölcsönhatások és spinmodellek

Az Einstein–de Haas-kísérletből tudjuk, hogy a ferromágneses anyagok mágneses momentuma nem az elektronok pályaperdületétől, hanem az ún. spintől származik. A spin fogalmát a relativisztikus kvantummechanika tisztázta: a spin is perdület jellegű mennyiség, de a pályaperdülettől eltérően nem a részecske sebességével kapcsolatos. Az elektron spinje feles, ami azt jelenti, hogy tetszőleges irányra nézve két spinállapota (±½ vagy ↑/↓) lehetséges. Egy atomban lévő elektronok spinjei a kvantummechanika szabályai szerint összeadódva meghatározzák az atom spinjét (S) és spin mágneses momentumát: M=gµBS, ahol g@2 az ún. giromágneses állandó, µB pedig az elemi mágneses momentum (Bohr-magneton). Bár egy fém vegyértékelektronjai nagy tértartományra (szabályos rácsnál az egész rácsra) kiterjednek, többnyire megfelelő az a leírás, hogy az atomoknak lokális spin mágneses momentumai vannak, amelyek iránya tetszőleges lehet (klasszikus spinvektorok).

Ha az atomi momentumok nagysága és iránya (a mérés időátlagában) megegyezik, akkor ferromágneses (FM) rendről, ha a momentumok alternálva két ellentétes irányba mutatnak, akkor antiferromágneses (AFM) rendről beszélünk. Ezeken felül természetesen még sok egyéb mágneses rendeződésű anyag létezik, például a ferrimágnesek és a mágneses csavarszerkezetek. A ferromágnesekben nagyobb méretű egyező irányítottságú tartományok, ún. mágneses domének találhatók. Egy makroszkopikus minta mágneses momentumának átfordulása (átmágneseződés) az individuális domének átbillenése és a doménfalak mozgása révén megvalósuló komplex folyamat. Ennek következménye például a Barkhausen-zaj.

Már a 20. század első harmadának végére nyilvánvalóvá vált, hogy a kollektív mágnesség eredete a kvantummechanikai eredetű kicserélődési kölcsönhatás. Az izotrop kicserélődési kölcsönhatás a két spin-momentum irányvektorainak skalárszorzatával arányos, -J12S1.S2, ahol J12>0 esetén a csatolás ferromágneses, J12<0 esetén antiferromágneses. Alapvető jelentőségű a mágneses momentumok közötti hosszú távú dipól–dipól kölcsönhatás, ami a doménszerkezet kialakulásáért felelős, illetve véges méretű mágnesekben a minta alakjától függő anizotrópia energia forrása. Ferromágneses vékonyrétegekben a mágneses dipól–dipól kölcsönhatás a mágnesezettség síkkal párhuzamos irányát preferálja, és az energia arányos a rétegvastagsággal. Az anizotrópia másik forrása a relativisztikus eredetű spin–pálya kölcsönhatás. Szemléletesen úgy fogalmazhatunk, hogy az elektromosan töltött, mozgó elektron által keltett mágneses tér kölcsönhat a spintől származó mágneses momentummal. A magnetokristályos anizotrópia tömbi mágnesekben is jelen van, de a vékonyrétegek és nanorészecskék (határ)felületein meghatározó járulékot adhat a rendszer energiájához. Leggyakrabban az egytengelyű anizotrópia Ka(Sz)2 modelljét használjuk, ahol Ka<0 (>0) a spinek felületre merőleges (a felülettel párhuzamos) beállását preferálja. A H külső mágneses tér hatását a –H.M Zeeman-energia írja le.

A szokásos spinmodellek a fenti kölcsönhatásokat tartalmazzák. A paramétereket (atomi mágneses momentumok, kicserélődési kölcsönhatás együtthatói, anizotrópia-állandó) a kísérleti adatokból vagy kvantummechanikai számításokból lehet megkapni. A rendszer mágneses szerkezete és mágneses dinamikája a statisztikus fizika eszközeivel (átlagtér-elmélet, Monte Carlo-szimulációk vagy a spinrendszer időfejlődését leíró Landau–Lifshitz–Gilbert-egyenlet) modellezhetők. A spinmodellek segítségével a mágneses jelenségek széles skálája írható le. Példaként említjük a doménstruktúrák kialakulását és mozgását, termálisan aktivált átmágneseződési folyamatokat legkülönbözőbb geometriájú mintákban, a vékonyrétegek vastagság- és hőmérsékletfüggő spinátfordulását vagy az FM–AFM-határfelület jelenlétében létrejövő kicserélődési eltolódás (exchange bias) jelenségét (Nowak, 2007)

Nem csoda, hogy az atomi spindinamika és mikromágneses szimuláció a nanomágnesség kutatásának rendkívül elterjedt, a technológiai fejlesztéseket közvetlenül szolgáló elméleti eszköze lett.

Szuperparamágnesség
és mágneses adattárolás

A ferromágnesek egyik legjellegzetesebb tulajdonsága, hogy a Curie-hőmérséklet alatt a mágnesezettség hiszterézist mutat a külső mágneses tér függvényében. Az M(H) hiszterézisgörbe három alapmennyisége az MS= M(H→∞) szaturációs mágnesezettség, az MR=M(H=0) remanens mágnesezettség és a HC koercitív tér, amelyre M(HC)=0. A kemény mágneseket nagy, a lágy mágneseket kis koercitív tér jellemzi. Megjegyezzük, hogy paramágnesek esetében HC=0, és a szaturációs mágnesezettség általában jóval kisebb, mint a ferromágneses anyagoké.

A ferromágneses részecskék D átmérőjének csökkenésével a koercitív tér jellegzetes változást mutat: először növekszik, tipikusan DS~50-100 nm-nél maximumot ér el, majd meredeken csökken, és Dp~10-15 nm alatt eltűnik, azaz a rendszer paramágneses jellegű lesz. D>DS esetén a nanorészecske több domént tartalmaz (multidomén szerkezet), D<DS esetén a nanorészecske uniform mágnesezettségű (egy-domén állapot). Egy ilyen nanorészecskére két, ellentétes mágneses momentumú (meta)stabil állapot jellemző. A két állapot közötti átmenethez KaV nagyságú energiabarriert kell legyőzni, ahol Ka az uniaxiális anizotrópia konstans és V a részecske térfogata. A termálisan aktivált átmenet időállandóját, a Néel-féle relaxációs időt, a Néel–Arrhenius-törvény alapján lehet meghatározni: t=t0exp(KaV/kBT), ahol t0 anyagi állandó, kB a Boltzmann-állandó és T a hőmérséklet. Ha a részecske elegendően kicsiny, azaz D<Dp, akkor külső tér nélkül is sok átbillenés következik be a két stabil állapot között a mérés tm átlagos időtartama alatt, tehát az átlagos (mért) mágneses momentum zérus. Ezt nevezzük szuperparamágneses állapotnak. A szokásos paramágneses viselkedéstől az különbözteti meg, hogy a szaturációs mágnesezettség, ill. a mágneses szuszceptibilitás a ferromágnesekéhez hasonló nagyságú. A szuperparamágnesek jellemző mennyisége a TB blokkolási hőmérséklet, amely fölött a koercitív tér eltűnik. Ennek meghatározó egyenlete: TB = KaV/kBln(tm/t0) ~20-25 KaV/kB. Szuperparamágneses vas-oxid nanorészecskéket ígéretesen használnak orvosbiológiai és gyógyászati alkalmazásokban, például MRI-kontrasztanyagként, sejtek, fehérje- és DNS-molekulák szétválasztására, hatóanyag-molekulák célzott eljuttatására a szervezetbe és daganatos sejtek hipertermiás elpusztítására.

Az ultranagy sűrűségű mágneses adattárolás a mágneses bit méretének csökkentésével érhető el. Ennek azonban határt szab a szuperparamágneses viselkedés, hiszen a blokkolási hőmérséklet fölött a beírt információ elvész. A magas blokkolási hőmérséklet és kis részecskeméret eléréséhez a mágneses anizotrópia növelésére van szükség. Ezenkívül a szórt mágneses dipóltér destabilizáló hatását is minimalizálni kell, ami úgy érhető el, hogy a bitek mágnesezettségét a felületre merőlegesen állítjuk. Ezt nevezzük merőleges mágneses adattárolásnak (perpendicular magnetic recording – PMR), amely 2005-től fokozatosan kiszorította a korábbi hosszirányú mágneses adattárolást (longitudinal magnetic recording – LMR). A merőleges adattároláshoz tipikusan réteges FePt-nanorészecskéket alkalmaznak, mivel a FePt-ötvözetet a vas- és platinarétegekre merőleges, nagy anizotrópia-energia és nagy mágneses momentum jellemzi. Ez utóbbi szükséges ahhoz, hogy a bitek átbillentésekor minél kisebb külső teret kelljen alkalmazni. A közeljövőben várható az ún. HAMR- (heat-assisted magnetic recording) technológia elterjedése, ahol az információ írásához a bitet egy fókuszált lézernyalábbal felmelegítik. Az igen rövid időre paramágneses állapotba kerülő nanorészecskéket már kis mágneses térrel át lehet mágnesezni. A Seagate Technology cég 2012 márciusában 1 terabit/négyzethüvelyk (1 terabit = 10¹² bit) adattárolási sűrűséget ért el a HAMR-technológia alkalmazásával (Seagate, 2012).

Spinfüggő transzport nanokontaktusokban

A nanoméretű heterogén mágneses rendszerek elektromos vezetési jelenségeiben nagy jelentőséget kap az a tény, hogy a különböző spinű elektronok vezetési tulajdonságai különböznek, azaz a transzport spinfüggő. Ezt a tulajdonságot használja ki a töltéstranszport helyett a spintranszportot, illetve spininformáció-átvitelt kutató és alkalmazó tudomány, a spintronika, amely értelemszerűen sok átfedést mutat a nanomágnességgel.

A kereskedelemben kapható számítógép-merevlemezek olvasófejei manapság szinte kizárólag az óriás mágneses ellenálláson (giant magnetoresistance – GMR) alapuló technológiát alkalmazzák. A jelenség felfedezéséért Albert Fert és Peter Grünberg 2007-ben fizikai Nobel-díjat kaptak. A GMR-jelenséget először alternáló ferromágneses-nemmágneses (FM–NM) rétegekből álló multirétegekben mutatták ki, de gyakorlati alkalmazására a spinszelepnek nevezett eszköz révén került sor. A spinszelep lelke egy rögzített mágneses orientációjú és egy, a külső mágneses tér által irányított, szabad ferromágneses réteg, amelyeket egy nemmágneses (spacer) réteg választ el. A két FM-réteg egyirányú vagy ellentétes mágneses orientációja esetén az eszköz elektromos ellenállása jelentősen megváltozik, többnyire az egyirányú esetben kisebb. Az olvasónak ajánlom Bakonyi Imre és munkatársai (2008), valamint Cserti József (2008) kiváló magyar nyelvű összefoglalóit a GMR részletesebb leírásáról és fizikai magyarázatáról. Itt csupán azt említjük meg, hogy a spacer rétegnek elegendően (néhány nm) vékonynak kell lennie ahhoz, hogy az elektronok spinje az áthaladás során ne forduljon át. A GMR tehát olyan tipikus méreteffektus, amelyekről a bevezetőben említést tettünk.

A merevlemez olvasófeje előtt elhaladó bit mágneses tere a szabad FM-réteg mágneses irányán keresztül változatja a spinszelep ellenállását, ami az átfolyó áramerősséggel könnyen kimérhető. A GMR-alapú olvasófejek elterjedése annak köszönhető, hogy jóval érzékenyebbek, mint a korábbi induktív vagy az anizotrop mágneses ellenálláson alapuló fejek, így lényegesebben nagyobb adattárolási sűrűség esetén alkalmazhatók. GMR-alapú eszközöket sok helyen

használnak, ahol a mágneses tér érzékeny mérésére van szükség (mágneses szenzorok).

Fölvetődik a kérdés, hogy a spinszelepen átfolyó áram megváltoztathatja-e a két FM-réteg relatív mágneses orientációját. Elméleti megfontolásokból következik, hogy egyfajta spinbeállású elektronok árama (spin-polarizált áram) egy FM-rétegen áthaladva a réteg mágnesezettségét átfordíthatja. Ezt nevezzük spinnyomaték-átvitelnek (spin-torque transfer), ugyanis a jelenség az áramot képviselő elektronok és az atomok összspinjének megmaradásán alapul, miközben a kölcsönhatást a kvantummechanikai kicserélődés közvetíti. A spinszelep megfelelő beállításával (például a spacer réteg vastagságával) megvalósítható, hogy az átfolyó áram irányától függően a két FM-réteg egyirányú vagy ellentétes irányú mágneses beállása stabilizálódjon. A gyakorlatban a spacer rétegben fém helyett valamely szigetelőanyagot (például alumínium-oxidot, magnézium-oxidot) alkalmaznak. A szigetelőn keresztül történő alagutazás (a kvantummechanikai alagúteffektus révén megvalósuló transzport) esetén fellépő, GMR-rel analóg jelenséget alagutazó mágneses ellenállásnak (tunneling magnetoresistance – TMR) nevezzük. A mágneses alagútkontaktusok (magnetic tunneling junction – MTJ) nagyobb érzékenységűek és kevésbé hőmérsékletfüggőek, mint a GMR-spinszelepek, ezért kitűnően alkalmazhatók nem felejtő, véletlen hozzáférésű memóriaként (magnetic random access memory – MRAM). Az Everspin Technologies cég 2012 végén egy 64 Mbit kapacitású, spinnyomaték elven működő MRAM- (ST-MRAM) memóriaegység piacra dobását jelentette be (Everspin, 2012). Az ST-MRAM az elektronikai eszközökben használt flash memóriák komoly vetélytársa lehet a jövőben.

Spinspirálok és skyrmionok –
egy érdekes kölcsönhatás következményei

A 2000-es évektől a spinpolarizált pásztázó alagútmikroszkóp (spin-polarized scanning tunneling microscope – SP-STM) technika segítségével a felületi mágneses struktúrák atomi felbontású detektálása és karakterizálása vált lehetővé. Az STM a minta fölött néhány nm távolságban mozgatott tű és a minta közötti áramot detektálja az elektromos előfeszítés függvényében, így részletes információt szolgáltat a minta felületének elektronállapotairól térben és energiában lokális felbontásban. Ha a tű mágneses, az alagutazó elektronok spinje a tű mágnesezettsége szerint polarizálódik, és az áramerősség a minta megfelelő polarizációjú elektronállapotainak sűrűségével lesz arányos. A tű mágneses irányának változtatásával kapott kontrasztképek analíziséből lehet következtetni a minta mágneses szerkezetére. A módszer nagy előnye, hogy igen nagy, lényegében atomi szintű felbontás érhető el (Wiesendanger, 2009). Jó példa erre, hogy a wolfram (110) Miller-indexű felületére felvitt ultravékony Fe-filmek SP-STM-vizsgálatából meghatározták a doménfalak vastagságát, és monorétegre ~1 nm, míg két atomi rétegre ~4 nm vastagságú falat kaptak. Ezeket a meglepően kis értékeket a spinmodellszámítások kielégítő pontossággal igazolták.

SP-STM-mérésekből és kvantummechanikai számításokból is ismeretes volt, hogy a W(110) felületre felvitt Mn monoréteg atomi soronként alternáló, a felülettel párhuzamos irányú antiferromágneses rendeződést mutat. A későbbi, atomi felbontású SP-STM-képekből viszont azt lehetett megállapítani, hogy ezt a rendeződést modulálja egy kb. 6 nm hullámhosszú periodikus spinstruktúra úgy, hogy a mágneses momentumok soronkénti egyirányú rendje megmarad. Az STM tű mágneses irányának változtatásával ki lehetett mutatni, hogy az atomi mágneses momentumok a sorok tengelye körül körbefordulva kilépnek a felület síkjából (Bode et al., 2007). Ez a szerkezet a ciklois spinspirál, amelyet a 2. ábra stilizál.

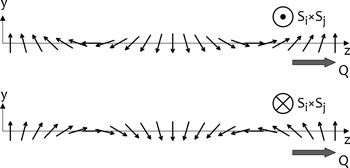
2. ábra • Kétféle forgási irányú, jobbra haladó ciklois spinspirál. A felső ábrán az egymást követő spinvektorok keresztszorzata a lap síkjába,

míg az alsó ábrán a síkból kifelé mutat. (Forrás)

Az ilyen csavarszerkezet kialakulása a korábban tárgyalt kölcsönhatásokkal nem magyarázható, ezért a spinmodellt ki kell terjeszteni az ún. Dzsalosinszkij (Dzyaloshinsky)-Moriya- (DM-) kölcsönhatással (Dzyaloshinsky, 1958; Moriya, 1960). Ez a kölcsönhatás arányos a két spinvektor keresztszorzatával, D12.(S1×S2), ahol D12 az ún. DM-vektor. A DM-kölcsönhatás a spinek egymáshoz viszonyított elfordulását preferálja úgy, hogy S1×S2 ellentétes irányú legyen D12-vel, hiszen így tud csökkenni a rendszer energiája. A DM-kölcsönhatás valójában a kicserélődési kölcsönhatás egy változata, ahol a spin–pálya kölcsönhatás szerepét is figyelembe vesszük. Érdekessége, hogy térbeli inverziószimmetriát mutató tömbi anyagokban eltűnik, de például komplex struktúrájú antiferromágnesek (például α-Fe2O3) „gyenge” ferromágnessége a DM-kölcsönhatással magyarázható. A spin–pálya kölcsönhatás indukálta anizotrópiához hasonlóan, sőt sok esetben annál nagyobb mértékben, a DM-kölcsönhatás szerepe a (határ)felület közelében megnő. Így van ez a Mn/W(110) monoréteg esetében is, ahol a felületi síkkal párhuzamos DM-vektorok a mágneses momentumok síkból való kifordulását okozzák.

A 2. ábra azt illusztrálja, hogy egy ciklois spinspirálnak kétfajta forgási iránya lehetséges. Mivel a két esetben a szomszédos rácspontok spinvektorainak keresztszorzata ellentétes irányú, a DM kölcsönhatás csak az egyik esetben csökkenti a rendszer energiáját, a másik esetben éppenséggel növelné azt. Ebből következik, hogy a DM-kölcsönhatás a spinspirál egy meghatározott forgási irányát preferálja. SP-STM-mérésekkel valóban megfigyelték, hogy a Fe2/W(110) ferromágneses film Néel típusú doménfalainak forgási iránya mindig ugyanaz, ami az előbb említett szimmetriasértés következménye. Ezt a gondolatot folytatva a BME Elméleti Fizika Tanszéken folyó elméleti vizsgálatok rámutattak, hogy az ultravékony mágneses filmek spinhullám-spektruma aszimmetrikus a haladás irányára nézve (Udvardi – Szunyogh, 2009).

Az utóbbi években a kutatások homlokterébe kerültek olyan nanoméretű, örvényszerű mágneses struktúrák, amelyek sok tekintetben hasonlatosak a nemlineáris térelmélet stabil részecskeszerű megoldásaihoz, amit Tony Skyrme magfizikus fedezett fel az 1960-as években. A mágneses skyrmionok (fonetikusan szkörmionok) folytonos deformációkkal szemben nagyfokú stabilitást mutatnak, szerkezetüknél fogva topologikusan védettek. A hőmérséklet és a mágneses tér megfelelő tartományában először tömbi mágnesekben (például MnSi, FeCoSi) mutattak ki skyrmion fázist, és azt elméletileg a DM-kölcsönhatás jelenlétével magyarázták. Kézenfekvő, hogy ultravékony rétegekben, ahol a DM-kölcsönhatás szerepe erőteljesebb, ugyancsak várható skyrmionok megjelenése. Ennek ellenére eddig csak Fe/Ir(111) monorétegen mutattak ki kísérletileg egy ún. nanoskyrmion-rácsot (Heinze et al., 2011), amely jellegében azonban jelentősen különbözik a tömbi rendszerekben megfigyelt, individuális skyrmionokból álló rácstól. Dr. Simon Eszter (BME Elméleti Fizika Tanszék) szilárdtestfizikai elektronszerkezet-módszerekkel kiszámította a hafnium hexagonális szoros pakolású (hcp) rácsának hatszöges szerkezetű, (0001) indexű felületére helyezett vas monoréteg spinmodell paramétereit, majd pedig spindinamika-szimulációkat végzett az alapállapoti spinkonfiguráció meghatározására. Az alapállapot ferromágneses ugyan, de a szimulációk több esetben a 3. ábrán látható skyrmion állapotot eredményezték. Ennek a spinmintázatnak az energiája nem sokkal magasabb, mint a ferromágneses alapállapoté, így a vékonyréteg kísérleti kezelésétől függően nagy valószínűséggel előfordulhat. A Fe/Hf(0001) monoréteg skyrmionja kb. 3×3 nm méretű, és szerkezetére jellemző, hogy a skyrmion középpontján bármely irányból áthaladva a spinek iránya 2p szöget jár körbe.

3. ábra • Számítógépes szimulációval kapott skyrmion állapot Fe/Hf(0001) monorétegben. A gömbök a vasatomok, a nyilak a mágneses momentumok irányát mutatják. (Dr. Simon Eszter számolása, BME Elm. Fiz. Tsz., 2013)

A Nobel-díjas Albert Fert és munkatársai nemrég megjelent cikkükben tárgyalják a mágneses skyrmionok alkalmazási lehetőségeit (Fert et al., 2013). Kétségtelen, hogy a néhány nm átmérőjű és egymástól 10–20 nm távolságban elhelyezkedő felületi skyrmionok a jelenleg ismert maximális adattárolási sűrűséget legalább két nagyságrenddel növelhetnék. Fert és munkatársai számítógépes szimulációkkal vizsgálták a skyrmionok mozgását áram hatására egy nanoszalagban. Megállapították, hogy a skyrmionok a doménfalakhoz hasonló sebességgel mozgathatók, viszont ehhez jóval kisebb áram szükséges, mint a doménfalak esetében. Ezek alapján ők nagy reményt fűznek a mágneses skyrmionok alkalmazásához az ultrasűrűségű adattárolás és logikai eszközök technológiája terén.

A fenti példa is meggyőzően bizonyítja, hogy a nanomágnesség dinamikusan fejlődő, az alap- és alkalmazott kutatások fókuszában álló terület, amelytől a jövőben is várhatunk a tudományt és társadalmat egyaránt gazdagító felfedezéseket.
 

Köszönetemet fejezem ki kollégáimnak, Dr. Udvardi Lászlónak, Dr. Újfalussy Balázsnak és Dr. Palotás Krisztiánnak, valamint édesapámnak, id. Dr. Szunyogh Lászlónak a cikk kéziratának gondos átolvasásáért és értékes tanácsaikért, illetve Dr. Simon Eszternek, hogy folyó kutatásainak egy szép eredményét (3. ábra) rendelkezésemre bocsátotta.
 

Kulcsszavak: nanomágnesség, mágneses nanoszerkezetek és nanorészecskék, mágneses kölcsönhatások, spinmodellek, szuperparamágnesség, ultranagy sűrűségű mágneses adattárolás, spintronika, óriás mágneses ellenállás, spinnyomaték-átvitel, Dzsalosinszkij–Moriya-kölcsönhatás, spinspirálok, skyrmionok
 

IRODALOM

Bakonyi Imre – Simon Eszter – Péter László (2008): Az óriás mágneses ellenállás felfedezése (1988) – A spintronika nyitánya – A 2007. évi fizikai Nobel-díj és háttere. Fizikai Szemle. LVIII, 2, 41–45. • WEBCÍM

Bode, Matthias et al. (2007): Chiral Magnetic Order at Surfaces Driven by Inversion Asymmetry. Nature. 447, 190–193. doi:10.1038/nature05802

Cserti József (2008): Nobel-díj az ellenállásért. Természet Világa. 139, 4. • WEBCÍM

Dzyaloshinsky, Igor E. (1958): A Thermodynamic Theory of ”Weak” Ferromagnetism of Antiferromagnets. Journal of Physics and Chemistry of Solids. 4, 241–255.  DOI:10.1016/0022-3697(58)90076-3

Everspin (2012): Spin-Torque MRAM. • WEBCÍM

Fert, Albert et al. (2013): Skyrmions on the Track. Nature Nanotechnology. 8, 152–156. doi:10.1038/nnano.2013.29

Heinze, Stefan et al. (2011): Spontaneous Atomic-scale Magnetic Skyrmion Lattice in Two Dimensions. Nature Physics. 7, 713–718. doi:10.1038/nphys2045 • WEBCÍM

Moriya, Tỏru (1960): Anisotropic Superexchange Interaction and Weak Ferromagnetism. Physical Review. 120, 91–98. DOI: 10.1103/PhysRev.120.91

Nowak, Ulrich (2007): Classical Spin Models. In: Helmut Kronmüller – Stuart Parkin (eds.): Handbook of Magnetism and Advanced Magnetic Materials. Vol. 2. 858–876.

Seagate (2012): Seagate Reaches 1 Terabit Per Square Inch Milestone In Hard Drive Storage With New Technology Demonstration. • WEBCÍM

Skomski, Ralph (2003): Nanomagnetics. Journal of Physics: Condensed Matter. 15, R841–R896. doi: 10.1088/0953-8984/15/20/202

Udvardi László – Szunyogh László (2009): Chiral Asymmetry of the Spin-wave Spectra in Ultrathin Magnetic Films. Physical Review Letters. 102, 207204 (4) DOI:10.1103/PhysRevLett.102.207204 • WEBCÍM

Wiesendanger, Roland (2009): Spin Mapping at the Nanoscale and Atomic Scale. Review of Modern Physics. 81, 4, 1495–1550.
 

LÁBJEGYZET

1 A végleges kézirat 2013. júniusi beküldése után született új irodalmi eredmények néhány vonatkozásban túlmutatnak a tanulmányban szereplő megállapításokon. <