Munkánk célja, hogy bemutassuk a Petri-hálók felhasználási lehetőségeit a modellezés és diagnosztika területén. Bemutatjuk technológiai rendszerek egy lehetséges modellezési formáját normál és hibás működésnél, hierarchikus színezett Petri-hálókat felhasználva. Bemutatjuk a folyamat modellje és a naplófájlban tárolt tracek összehasonlítása alapján a hiba feltárásának folyamatát. Javaslatot teszünk a folyamat hibamentes működését leíró referenciamodell és egy tényleges működés alapján származtatott modell összehasonlításának módszerére gráfelméleti alapokon.

Bevezetés

A technológiai rendszerek diagnosztikai vizsgálata során a modellalapú módszerek igen népszerűek és széles körben alkalmazottak kedvező tulajdonságaik miatt (lásd van der Aalst et al., 2004; Hangos – Cameron, 2001). A diszkrét eseményű rendszerek területén kifejlesztett eszközöket és módszereket alkalmazva, a kapott modell jól használható a vizsgált rendszer működésének és rendszertulajdonságainak vizsgálatára (lásd Hangos et al., 2001, Werner et al, 2011; Werner et al, 2012). Ezeknek a modelleknek egyik népszerű formája a Petri-háló (lásd Jensen, 1994; Murata, 1989). Közleményünk célja, hogy új megközelítésekben mutassuk be a Petri-hálók felhasználási lehetőségeit a modellezés és diagnosztika területén.

A diagnosztikai vizsgálatokhoz elkészítjük a folyamat működését leíró Petri-háló alapú modellt, mely a vizsgált folyamatban lejátszódó eseményeket és azok előfeltételeit, illetve következményeit emeli ki. A másik fontos kiindulási eszköz a rendszer működéséről adatokat tartalmazó eseménynapló (naplófájl). Az általunk vizsgált diagnosztikai módszerek ezeknek a modelleknek és naplófájloknak a különböző módon történő összehasonlítását végzik el.

Modellezés Petri-hálók segítségével

A Petri-háló diszkrét állapotú és diszkrét idejű rendszerek leírására alkalmas eszköz, melyet Carl Adam Petri német matematikus fejlesztett ki soros automaták kommunikációjának modellezésére az 1960-as évek elején. A módszer kidolgozása óta a Petri-hálókat számos formában fogalmazták meg, és modellezési képességeik bővítése érdekében sokféle irányban fejlesztették tovább.

Kutatásaink során elsősorban az eredeti definíciónak megfelelő, ún. alacsony szintű hálókat, ileltve a hierarchikus, színezett hálókat alkalmaztuk, így a következőkben ezek definícióját ismertetjük vázlatosan (Murata, 1989); Jensen, 1994 alapján.)

Egy alacsony szintű Petri-háló a következő ötössel adható meg: PN = (P, T, A, w, m), ahol

• P : helyek halmaza;

• T : átmenetek halmaza;

• A ⊆ (P ×T) ∪ (T×P) az élek halmaza;

• w : A → N⁺ az élek súlyait megadó függvény;

• m : P → N a jelzőpontok eloszlását megadó függvény.

A modellezés során a rendszerből a lejátszódó eseményeket vagy műveleteket, és ezek előfeltételeit és következményeit emeljük ki. A Petri-hálóban az eseményeknek az átmenetek, az előfeltételeknek, következményeknek a helyek felelnek meg, míg a köztük lévő kapcsolatot az élek adják meg. A hálót nagyon gyakran gráfként jelenítik meg, ahol az átmeneteket téglalappal, a helyeket körökkel, az éleket pedig nyilakkal szimbolizálják. A vizsgált rendszer működését a háló szimulációjával vizsgálhatjuk. Az átmenetek lejátszódásához, a valós rendszerhez hasonlóan, az előfeltételeiknek teljesülniük kell, melyeket jelzőpontok, ún. tokenek hozzárendelésével lehet szimbolizálni. A modellezett rendszertől függően szükség lehet arra, hogy egy átmenet lejátszódásához az előfeltételi helyén kettő vagy több token (például munkadarab) legyen. A w élfüggvény ezeknek a helyzeteknek a kezelésére alkalmas, míg az m jelzőponteloszlás-függvény a tokenek aktuális eloszlását adja meg.

Míg az alacsony szintű Petri-hálókban a jelzőpontok megkülönböztethetetlenek, addig az ún. színezett Petri-hálókban a jelzőpontokhoz színeket, vagyis a tokenek által reprezentált diszkrét értékű adatoknak megfelelő típusokat rendelhetünk. E módosítás miatt további fogalmakat, így a jelzőpontok színeinek kiértékelését elvégző, élekhez rendelt ívkifejezéseket, valamint az átmenetekhez tartozó őrfüggvényeket is be kell vezetni. A színezett Petri-hálók definíciója Kurt Jensen művében (1994) található meg részletesen. A színezett Petri-hálók segítségével a modellek szerkezete sokkal egyszerűbb, átláthatóbb lesz, a pontos értelmezhetőséghez azonban szükség van az ívkifejezések és az őrfüggvények ismeretére is.

Az ún. hierarchikus hálókban lehetőség van alhálók beépítésére, ami egyrészt egyszerűsíti a modellezési munkát és a főháló szerkezetét, másrészt viszont nehezíti a modell részletes értelmezését. Petri-hálóban az időkezelés általában az átmenetek és helyek sorrendiségében jelenik meg, de létezik a hálónak olyan továbbfejlesztése, melyben az idő közvetlenül is megjelenik.

A leírtakból látható, hogy a különböző típusú Petri-hálók kiválóan alkalmasak diszkrét eseményű és idejű technológiai rendszerek működésének elemzésére, mind szimuláció, mind a felsorolt rendszertulajdonságok vizsgálata alapján.

Technológiai rendszerek normál
és hibás működésének modellezése
Petri-háló segítségével

Kutatásunk egyik célja egy olyan, diszkrét eseményű technológiai rendszerek állapotainak széles körű feltárására alkalmas Petri-háló alapú modellezési eljárás megalkotása volt, amely egyaránt lehetővé teszi a normál üzemelés, valamint különböző hibalehetőségeket tartalmazó hibás működés lejátszódásának leírását is.

Első lépésként, a műveletek helyes lejátszódási sorrendjének és a köztük lévő kapcsolatoknak ismerete alapján elkészítjük a vizsgált rendszer ún. normál referenciamodelljét, mely a vizsgált rendszer hibamentes működésének felel meg. Összetett, nagy technológiai rendszerek modellezése esetén segíti az elkészült modell áttekinthetőségét, ha a szorosabban összetartozó technológiai lépéseket alhálókba szervezzük, azaz hierarchikus hálót alakítunk ki.

Következő lépésként különböző, ismert hibák rendszerbe történő integrálását végeztük el, melynek eredményképpen különféle hibás működési módok vizsgálata válik lehetségessé. A hibalehetőségeknek Petri-háló alapú modellben való figyelembe vételét általában hibahelyek és/vagy hibaátmenetek hálóba történő beépítésével szokták elvégezni (Blanke et al., 2006), ez azonban jelentősen növelheti a háló méretét és bonyolultságát. Ezt elkerülendő, a hibáknak a modellbe történő integrálását egy új, egyedi ötlet alapján hajtottuk végre (Márczi et al., 2011, Márczi et al., 2012). Ennek lényege, hogy a hibáknak a referenciamodellbe történő integrálását a színezett Petri-háló elemeihez rendelhető függvények és utasítások segítségével oldottuk meg. Az átmenetekhez rendelt ellenőrző függvények a felhasználó által előre definiált valószínűséggel térnek vissza hibás vagy hibamentes működésre utaló értékkel. Az átmenetek és helyek között lévő irányított élekhez tartozó feltételes utasításokba kódoltuk be, hogy mi játszódjon le hibás működés esetén. Az, hogy melyik feltételes utasítás játszódik le, az a megelőző átmenethez rendelt ellenőrző függvény visszatérési értékétől, vagyis a token színétől függ. A beépített függvények felelnek azért is, hogy egy rendszerleállást eredményező hiba esetén a háló tokeneloszlása a kezdeti tokenelosztással egyezzen meg, vagyis inicializációs állapotba kerüljön a rendszer. A hibák bekövetkezése tehát, a rendszer valós működéséhez hasonlóan véletlenszerű, előfordulásukat pedig egy, a felhasználó által paraméterezett valószínűségi függvény szabályozza. A gyakoriságok beállításánál, a gyártórendszer működése során előálló naplófájlokból adatbányászati elemzések révén kapott hibastatisztikák lehetnek segítségünkre. Azt a modellt, amely már a különféle hibás működéseket is tartalmazza, kiterjesztett referenciamodellnek hívjuk.

Az 1. ábrán egy olyan technológiai rendszer Petri-háló alapú normál referenciamodelljének felső szintje látható, mely négy alhálóba összevont technológiai lépésből áll. A 2. ábrán az egyik alháló látható a hibalehetőségek integrálása után.

Diszkrét eseményű
modellstruktúra-identifikáció

A Petri-hálók segítségével megadott diszkrét eseményű rendszerek struktúraidentifikációjához modellalapú diagnosztika céljából felhasználhatjuk a folyamatbányászat (van der Aalst et al., 2007; van Dongen et al., 2005) fogalmait és eszközeit. Ehhez szükséges a lehetséges hibamódok feltárása, majd a normál működési mód és a hibás működési

mód(ok) modellezése (Werner et al., 2011), amelyre utaltunk a 3. fejezetben. A folyamatbányászat (lásd ProM-rendszer [van Dongen et al., 2005]) lehetőséget biztosít arra, hogy folyamati adatokból (naplófájl) állítsunk elő Petri-háló modelleket (van der Aalst et al., 2004). Az adatok a naplófájlban speciális formátumban (MXML-formátum) kell, hogy rendelkezésre álljanak. Egy eseménynapló tartalmazza eseménysorozatok egy halmazát (trace), amelyek mindegyike speciális viselkedést ír le, amelyek között hibás eseményvégrehajtás is lehet. A modellek előállítására számos algoritmus létezik, mint például az alfa-algoritmus, a genetikus algoritmus vagy a heurisztikus eljárás stb. (van Dongen et al., 2005).

A valamely algoritmus által létrehozott folyamati modell ezek után összehasonlítható a referenciamodellel. Kérdés, hogy az előállított modell (lehet normál vagy hibás működést leíró) algráfja-e a referenciamodellnek. Ha ez igaz, akkor meg tudjuk mondani, hogy vajon a rendszer normális feltételek mellett zajlik-e, vagy izolálni tudjuk a hibát. Ha ez nem igaz, akkor új, lehetséges hibát fedeztünk fel.

Folyamatinformációk alapján generált
Petri-háló modellek felhasználása
diagnosztikai vizsgálatokhoz

A gyártórendszer működése során fellépő hibák súlyosságukat tekintve alapvetően háromfélék voltak:

• azonnali leállást eredményező súlyos hiba,

• selejtet eredményező hiba,

• leállást nem eredményező kisebb hiba.

Diagnosztikai vizsgálataink célja, hogy a vizsgált rendszer működése során szerzett információkból visszaállított hálót összehasonlítva az előzetes információk alapján felállított helyes és különböző hibás működéseket leíró hálókkal, következtessünk a technológiai rendszer működésének helyességére. Ezt a vizsgálatot kutatásaink során a Petri-hálók terében végeztük el, azaz a tényleges (esetleg ismert vagy ismeretlen hibát tartalmazó) működést leíró Petri-hálót összehasonlítjuk a rendszer normál referenciamodelljével, és a Petri-hálók gráftávolságát meghatározva következtetünk a normál működéstől való eltérés mértékére, azaz a hiba súlyosságára (Gerzson et al., 2011). Gráfok távolságának meghatározása legnagyobb közös részgráfjuk ismeretében az alábbi képlettel történhet (Bunke – Shearer, 1998):

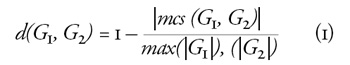
ahol |G| a G gráf csúcsainak számát, mcs(G1, G2) a G1 és G2 gráfok maximális közös részgráfját, míg d(G1, G2) a G1 és G2 gráfok távolságát jelöli. A maximális közös részgráf megkeresése általában algoritmikusan nehéz feladat, de az általunk összehasonlítani kívánt Petri-hálók csúcscímkézett gráfoknak tekinthetőek és az alkalmazott hibamodellezés miatt speciális szerkezetűek, így a gráftávolság számolása ebben az esetben algoritmikusan lényegesen egyszerűbb probléma.

Míg a gyártórendszerek különböző modelljeiként a komplex rendszerek esetén is jól átlátható hierarchikus, színezett Petri-hálókat célszerű használni, addig a gráfok szerkezeti analíziséhez, így a gráfösszehasonlításhoz is egyszintű (nem hierarchikus) és alacsonyszintű (nem színezett) hálókat kell alkalmazni. A hierarchikus és színezett hálóként felépített alapmodellt egy általunk fejlesztett Converter szoftver (Márczi et al., 2011) felhasználásával alakítjuk át ProM (van Dongen et al., 2005) szoftverrel megjeleníthető alacsonyszintű, egyszintű hálóvá, ahogy azt a 4. fejezetben már említettük.

Munkánk jelen szakaszában a technológiai rendszer működését a CPN-Tools-ban végzett szimulációval vizsgáltuk. A háló végrehajtása során a program lehetőséget ad a valós rendszerek működéséhez hasonló naplófájlok generálására. Ezek a naplófájlok időbélyeggel ellátva tartalmazzák a technológiai rendszerben vagy az azt szimuláló hálóban bekövetkező eseményeket, azok végrehajtóit. Ezeknek az adatoknak a segítségével lehet az adott működésnek megfelelő hálót visszaállítani, majd azt a normál referenciahálóval összehasonlítva a rendszer működési állapotát meghatározni. A vizsgált rendszerünk referenciamodellje és egy tényleges, a folyamat elején leállást okozó hibás működéshez tartozó modell alacsonyszintű hálója a 3. ábrán látható.

A két gráf távolsága a legnagyobb közös részgráf alapján meghatározva d1 = 0.69 értéknek adódik. Összehasonlításképpen az 1. táblázat két további esetben (leállást nem eredményező kis hiba, illetve leállást nem eredményező kis hiba, majd a folyamat végén leállást eredményező hiba) is mutatja a számolt gráftávolságok értékét.

Megállapítható, hogy ha a technológiai folyamatban csak egy kicsi, kezelhető hiba következik be, akkor a kapott gráftávolság értéke kicsi. Leállást eredményező hiba esetén annál közelebb lesz a kapott távolságérték 1-hez, minél korábban következett be a leállást eredményező hiba.

Konklúzió

Munkánkban összefoglaltuk azokat a lehetőségeket, amelyek felhasználhatóak lehetnek járműipari diagnosztikai területen. A folyamatok elemzéséhez egyrészt modelleket – itt a Petri-hálók kerültek alkalmazásra –, másrészt a folyamatok során rögzített naplófájlokat használtunk fel. Megmutattuk, hogy a diagnosztikai elemzésekhez normál referenciamodellt szükséges készíteni, ami célszerűen hierarchikus felépítésű, másrészt kiterjesztett referenciamodelleket, amelyek a lehetséges hibákat is megjelenítik. Vizsgáltuk, hogy diszkrét eseményű rendszerek struktúra-identifikációjához hogyan használhatók a folyamatbányászat eszközei. Bemutattunk egy módszert a referenciamodell és a naplófájlból előállított helyes és hibás működéseket leíró modellek összehasonlítására. A bemutatott módszereket járműipari területen vizsgáltuk, és megállapítottuk, hogy ezen speciális területeken is van létjogosultsága a modellezési, naplófájl-feldolgozási, az összehasonlítási műveleteknek, ha azokat elsődlegesen hibadiagnosztikára akarjuk használni.
 

Ez a munka a Magyar Állam és az Európai Unió pénzügyi támogatásával valósult meg a TÁMOP-4.2.1/B-09/1/KONV-2010-0003 projekt keretén belül.
 

Kulcsszavak: folyamat, modellezés, Petri-háló, hibadiagnosztika, járműipar
 

IRODALOM

Blanke, M. – Kinnaert, M. – Lunze, J. – Staroswiecki, M. (2006): Diagnosis and Fault-tolerant Control. Springer-Verlag

Bunke, H. – Shearer, K. (1998): A Graph Distance Metric Based on Maximal Common Subgraph. Pattern Recognition Letters. 19, 255–259.

Gerzson M. – Leitold A. – Hangos K. M. (2011): Model Based Process Diagnosis Using Graph Methods. Factory Automation 2011 Conference, Győr, Hungary, 62–70.

Hangos K. M. – Cameron, I. T. (2001): Process Modelling and Model Analysis. Academic Press, London

Hangos K. M. – Lakner R. – Gerzson M. (2001): Intelligent Control Systems: An Introduction with Examples. Kluwer Academic Publisher, New York

Jensen, K. (1994): Coloured Petri Nets. Springer-Verlag

Márczi, B. – Gerzson, M. – Leitold, A. (2011): Diagnostic Investigations Based on the Petri Net Model Generated from the Process Information. Hungarian Journal of Industrial Chemistry. 39, 1, 133–139.

Márczi B. – Leitold A. – Gerzson M. (2012): Diagnosis of Technological Systems Based on Their Colored Petri Net Model. 7th Vienna Symposium on Mathematical Modelling, Wien, Austria, ARGESIM Report S38.

Murata, T. (1989): Petri Nets: Properties, Analysis and Applications. Proceedings of the IEEE. 77, 4, 541–580.

van der Aalst, W. M. P. et al. (2007): Business Process Mining: An Industrial Application. Information Systems, 32, 5, 713–732.

van der Aalst, W. M. P. – Weijters, A. J. M. M. – Maruster, L. (2004): Workflow Mining: Discovering Process Models from Event Logs. IEEE Transactions on Knowledge and Data Engineering. 16(9): 1128-1142 2004.

van Dongen, B. F. et al. (2005): The ProM Framework: A New Era in Process Mining Tool Support. ICATPN. 444–454.

Werner-Stark A. – Gerzson M. – Hangos K. M. (2011): Discrete Event Model Structure Identification Using Process Mining. Proceedings of the IASTED International Conference Modelling, Identification, and Control (MIC 2011), Innsbruck, Austria, 228–233, ISBN 978-0-88986-863-2

Werner-Stark A. – Dulai T. (2012): Agent-based Analysis and Detection of Functional Faults of Vehicle Industry Processes: A Process Mining Approach. 6th International KES Conference on Agents and Multi-agent Systems, Technologies and Applications KES-AMSTA 2012, Dubrovnik, Croatia, 25–27. 06. 2012.