|
Amennyiben a cellára nagyfeszültségű impulzus
formájában külső elektromos teret kapcsolunk, a tér hatására a
folyadék beláncosodik. Az ER-folyadék dielektromos permittivitása
megváltozik, ami a mérőcella kapacitásának változását vonja maga után.
Ez a kapacitásváltozás az oszcillátor frekvenciájának elhangolódását
okozza, amit egy frekvenciamoduláció (FM) analizátorral követünk.
A nagyfeszültségű négyszögimpulzust egy
tápegységből és egy nagyfeszültségű kapcsoló egységből álló
impulzusgenerátor állítja elő. A cella fegyverzetei között a kialakuló
elektromos térerősség 106 Vm-1 nagyságrendű. A Cb blokkoló kondenzátor
akadályozza meg, hogy a nagyfeszültségű impulzus az oszcillátor aktív
elemeire jusson. Ahhoz, hogy a Thomson-egyenlet, azaz f = (2π√LC)
alapján az oszcillátor frekvencia meghatározó eleme Cc legyen, a Cc <<
Cb feltétel teljesülése szükséges.
3.2. Reológiai vizsgálatok • Az
ER-folyadékok nyírás közbeni viselkedését egy elektroreológiai
feltéttel ellátott Anton Paar gyártmányú reométerrel (Physica MCR 301)
vizsgáltuk. Az ER-feltét lehetővé teszi, hogy a reológiai méréseket
elektromos tér alkalmazása mellett végezzük el. A minta két
párhuzamos, egy álló és egy forgó síklap (sík-sík geometria) között
helyezkedik el. A nagyfeszültségű négyszögimpulzust e két elektród
közé kapcsoljuk. Az elektródok között az elektromos térerősség a
dielektromos mérőberendezésnél alkalmazotthoz hasonlóan 106 Vm-1
nagyságrendű. A mérések során a nyírási sebesség 0,1 és 100 s-1 között
változott.
4. A kísérleti eredmények értelmezése
Az általunk végzett vizsgálatoknál a (4) egyenlet
alapján definiált paraméter értéke λ ≈ 0,01. Ez azt jelenti, hogy a
vizsgált ER-folyadékok szerkezetének kialakításában a hőmozgásból
eredő diffúzió szerepe nem elhanyagolható, ami a felhasznált SiO2-szemcsék
kis méretét tekintve nem meglepő.
A dielektromos mérőberendezéssel mért frekvenciaváltozást – ami
arányos a vizsgált folyadék permittivitás változásával – a
2. ábra
mutatja be. Két ismert dielektromos permittivitású anyaggal
végzett kalibráció után a mért frekvenciaváltozásból kiszámolható a
permittivitásváltozás. Az ábrán három 0,1 s időtartamú, azonos
amplitúdójú impulzussorozat hatása látható. Az impulzusok között
eltelt idő 0,1 s.
Az első impulzus bekapcsolásakor az oszcillátor
frekvencia exponenciális függvény szerinti csökkenése tapasztalható,
ami a láncosodás okozta permittivitásnövekedés következménye. Az
impulzus után az elektromos térerősség megszűnésével (E = 0, λ = 0) a
folyadék szerkezetét a hőmozgásból eredő diffúzió
határozza meg, azaz a létrejött láncos szerkezet elkezd szétesni. Ezt
a folyamatot a frekvencia növekedése (a permittivitás csökkenése)
jelzi. A további impulzusok hatására a folyadék permittivitása már
csak kisebb mértékben növekszik, hiszen a második és a harmadik
impulzus bekapcsolásakor a folyadék már tartalmaz láncokat.
Az ER-folyadékok dielektromos permittivitásának
időbeli változása a nagyfeszültségű impulzus hatásideje alatt (3.
ábra) egy kettős exponenciális alakú függvénnyel írható le a
legjobban (Jolly et al., 1999):
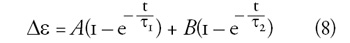
A fenti egyenletben Δε a folyadék impulzus előtti
dielektromos permittivitásához viszonyított permittivitásváltozás, t
az idő, A, B, τ1 és τ2 pedig illesztési
paraméter. A (8) egyenletben szereplő τ1 időállandó a
részecskék párképződését jellemző, (5) egyenlet alapján számolható τp
karakterisztikus időnek feleltethető meg. A τ2 időállandó
pedig a hosszú láncok kialakulásának karakterisztikus idejét adja meg.
Különböző rendszerek esetén a τ2 általában öt-tízszer
nagyobb, mint a párképződési időállandó (Ly et al., 1999).
A karakterisztikus idők meghatározásához az
ER-folyadékokra különböző amplitúdójú, 140 s időtartamú impulzusokat
kapcsoltunk (3. ábra). Ilyen hosszú impulzusok hatása alatt
körülbelül 90 s eltelte után a folyadék permittivitása már nem
növekszik, azaz a szerkezet állandósul. Nagyobb térerősségű impulzusok
nagyobb permittivitásváltozást okoznak, mivel λ növekedésével
egyre több részecske vesz részt a láncok
kialakításában. A térerősség növelése egy határon túl (E ≈ 6 MVm-1, λ
≈ 0,15) már nem okoz nagyobb permittivitásnövekedést. Ez azzal
magyarázható, hogy ekkora térerősség mellett a részecskék döntő
hányada már a láncos szerkezet tagja.
A két különböző viszkozitású szilikonolajból
készült folyadék esetén az illesztés alapján kapott időállandókat a
2. táblázat hasonlítja össze az (5) egyenlettel számolt
karakterisztikus időkkel. Annak ellenére, hogy a képletek csak
közelítő feltételek mellett érvényesek, az egyezés a mért értékekkel
jónak mondható.
A permittivitás-növekedés mértékét megbecsülhetjük
a Weijia Wen és munkatársai által elméleti megfontolások alapján
megadott formulákkal (Wen et al., 1997). Az izotrop ER-folyadék
dielektromos permittivitása az
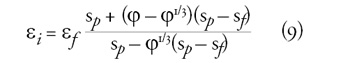
míg a teljes mértékben beláncosodott folyadéké az
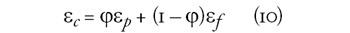
egyenlettel számolható, ahol j a diszpergált
szemcsék térfogattörtje. Az általunk vizsgált 2 térfogat%-os, η = 0,97
Pas viszkozitású szilikonolajból készült ER-folyadék dielektromos
permittivitása Δε = 0,021-el változott az E = 3,85 MVm-1 elektromos
térerősség hatására. Ugyanerre a rendszerre az említett (9) és (10)
egyenletekkel számolva Δε = 0,007 permittivitás-változás adódik, azaz
a formulák csak korlátozottan használhatók.
A nagyfeszültségű impulzusnak kitett szilikonolaj-SiO2 ER-folyadék
nyírás (g = 1 s-1) közbeni viselkedése a 4. ábrán látható. Az eltelt
időt a 30 s időtartamú, különböző amplitúdójú impulzusok
bekapcsolásától számítjuk. A nyírás alatt álló folyadék válaszideje az
1. táblázatban szereplő egyenlet alapján a nyírási sebesség
reciprokával egyenlő, azaz Tv = 1 s, míg a mérések alapján a válaszidő
Tv = 0,8 s. Kisebb nyírási sebesség mellett (g = 0,1 s-1) a számolt
karakterisztikus idő Tv = 10 s, a mérések szerint pedig Tv = 5,1 s.
Azaz az elméleti formula csak nagyságrendi becslésre használható.
Megállapítható, hogy az ER-folyadék válaszideje a nyírási sebesség
növelésével csökken.
Ahogy a 4. ábrán jól látható, az elektromos térerősség növelésével
adott nyírási sebesség mellett a folyadékban ébredő nyírási feszültség
megközelítőleg lineárisan növekszik. Ez eltér a folyadék dielektromos
permittivitásának a 3. ábrán bemutatott változásától. Ahogy azt
korábban említettük, a térerősség egy kritikus értékénél szinte az
összes részecske láncokba szerveződik, így a térerősség további
növelése nem okoz nagyobb permittivitásváltozást. A részecskék közötti
elektrosztatikus vonzóerő viszont növekszik, vagyis a láncokat egyre
nehezebb elszakítani, ami a nyírófeszültség növekedését jelenti.
5. Összefoglalás
Dielektromos permittivitást mérő berendezést építettünk
elektroreológiai folyadékok elektromos tér hatásideje alatti
láncosodásának vizsgálatára. Szilikonolaj és szilíciumdioxid-alapú
ER-folyadékokra megmértük a részecskék láncosodása okozta dielektromos
permittivitásváltozást.
A dielektromos mérési adatok kiértékelésénél kiszámítottuk a
párképződés és a hosszabb láncok kialakulásának karakterisztikus T1 és
T2 idejét. Az így nyert karakterisztikus idők jó egyezést mutattak az
irodalomból vett elméleti egyenletek alapján számolt adatokkal.
A vizsgált ER-folyadékokra meghatároztuk a viszkozitás időfüggését a
különböző külső elektromos terek esetén. Megállapítottuk, hogy a
viszkozitásmérésekből származtatott karakterisztikus idő (Tv)
nagyságrendileg egyezik az elméleti formulákkal számoltakkal.
A kutatási téma a Magyar Állam és az Európai Unió anyagi támogatásával
a TÁMOP-4.2.1/B-09/1/KONV-2010-0003 projekt keretén belül valósult
meg.
Kulcsszavak: elektroreológiai folyadékok, láncképződés,
dielektromos permittivitás
IRODALOM
Adolf, D. – Garino, T. (1995):
Time-Dependent Dielectric Response of Quiescent Electrorheological
Fluids. Langmuir. 11, 307–312.
Baxter-Drayton, Y. – Brady, J. F. (1996):
Brownian Electrorheological Fluids as a Model for Flocculated
Dispersions. Journal of Rheology. 40, 1027–1056.
Blackwood, K. M. – Block, H. – Pattray, P.
et al. (1994): The Polarization, Structuring and Rheology of ER
Fluids. In: Tao, R. – Roy, G. D. (eds.): Electrorheological Fluids.
World Scientific, Singapore
Bradley, P. A. – Jones, G. P. (1974): A
System for the Investigation of Nonlinear Dielectric Effects Using
Digital Techniques. Journal of Physics E: Scientific Instruments. 7,
449–452.
Brown, B. L. – Jones, G. P. – Davies, M.
(1974): Dielectric Measurements in the Presence of a Rectangular
Electric Pulse and Their Comparison with Electric Birefringence.
Journal of Physics D: Applied Physics. 7, 1192–1199.
Jolly, M. R. – Bender, J. W. – Mathers, R.
T. (1999): Indirect Measurements of Microstructure Development in
Magnetorheological Fluids. International Journal of Modern Physics B.
13, 2036–2043.
Klingenberg, D. J. – Zukoski, C. F.
(1990): Studies on the Steady-Shear Behavior of Electrorheological
Suspensions. Langmuir. 6, 15–24.
Ly, H. V. – Ito, K. – Banks, H. T. (1999):
Dynamic Simulation of the Temporal Response of Microstructure
Formation in Magnetorheological Fluids. In: Tao, R. – Roy, G. D.
(eds.): Electrorheological Fluids. World Scientific, Singapore
Martin, J. E. – Odinek, J. – Halsey, T. C.
et al. (1998): Structure and Dynamics of Electrorheological Fluids.
Physical Review E. 57, 1, 756–775.
Rzoska, S. J. – Zhelezny, V. P. (2004):
Nonlinear Dielectric Phenomena in Complex Liquids. (NATO Science
Series II: Mathematics, Physics and Chemistry) 157.
Schwarz, G. – Walther, P. (1985):
Experimental and Theoretical Studies on the Dielectric Field Effect of
an Alamethicin-Like Peptide in a Lipophilic Medium. Berichte der
Bunsengesellschaft für physikalische Chemie. 89, 491–500.
Wen, W. – Ma, H. – Tam, W. Y. et al.
(1998): Anisotropic Dielectric Properties of Structured
Electrorheological Fluids. Applied Physics Letters. 73, 21, 3070–3072.
Wen, W. – Men, S. – Lu, K. (1997):
Structure-Induced Nonlinear Dielectric Properties in
Electrorheological Fluids. Physical Review E. 55, 3, 3015–3020.
|