|
|
1860. január 27-én halt meg marosvásárhelyi
otthonában Bolyai János, a világhírű matematikus, a magyar tudomány
legnagyobb alakja. 1802. december 15-én született Kolozsvárott,
életének nagy részét Erdélyben töltötte. Úttörő volt a nemeuklideszi
geometria megalkotásában, felépítette az abszolút és a hiperbolikus
geometriát, melyek Eukleidész 5. posztulátuma figyelmen kívül
hagyásán, illetve tagadásán alapulnak. Munkájának jelentőségét
kortársai nem értették meg, halála után azonban nem sokkal megindult a
világhír felé. Hatására az axiomatikus gondolkodás széles körben
elterjedt, a matematika egésze átalakult, és az új gondolkodásmód
nyomot hagyott az egyetemes emberi kultúrán. Bolyai János halálának
emlékére a Magyar Tudományos Akadémia, a Pannon Egyetem Műszaki
Informatikai Kara és a Sapientia Egyetem 2010. augusztus 30. és
szeptember 4. között nemzetközi tudományos konferenciát rendezett,
melynek helyszíne Budapest és Marosvásárhely volt.
Milyen sors vár arra, aki megold egy kétezer éves problémát, és nem a
kor tudományos központjainak egyikében tevékenykedik, hanem azoktól
távol, egy valószínűtlen helyről adja jelét korszakalkotó
felfedezésének? Egy ilyen régi probléma megoldásának bejelentése
önmagában is gyanút kelt, hiszen a felvetéstől a megoldásig eltelt idő
túlságosan hosszú. Amit a sors Bolyai Jánosra kiszabott a párhuzamosok
kétezer éves problémájának megoldása után, nem egyszerűen mellőzés
vagy agyonhallgatás, hanem értetlenség és ledorongolás, éltében,
holtában egyaránt. Amikor Carl Friedrich Gauss kézhez vette Bolyai
János Appendix című művét, melyet János apja, Bolyai Farkas neki
megküldött, 1832. március 6-i válaszlevelében ezt írta: „Most valamit
fiad munkájáról. Ha azzal kezdem, hogy nem szabad megdicsérnem,
bizonyára egy pillanatra meghökkensz. Mást azonban nem tehetek: ha
megdicsérném, akkor magamat dicsérném, mert a mű egész tartalma, az
út, amelyet fiad követ, és az eredmények, amelyekre jutott, majdnem
végig megegyeznek részben már harminc-harmincöt év óta folytatott
meditációmmal.” Egy másik negatív vélemény ugyanennek az évnek
szeptemberéből való, Gustav Adolf Geisinger írta, a bécsi cs. és k.
Mérnök Akadémia felsőbb matematikaprofesszora, Bolyai
szabadságkérelmének elbírálásakor: „Végül az alárendelt [véleményíró]
nem kerülheti el, hogy ne méltányolja a szorgalmat és az
éleselméjűséget, amellyel a szerző egy egyszer elfogadott hipotézisre
egész munkáját felépítette, és az elkövetkezőkben azt kívánja, hogy
gyümölcsözőbb témát válasszon.” További mélypontot jelent Péterfi
Károly református esperesnek, a Magyar Tudományos Akadémia levelező
tagjának bejegyzése a marosvásárhelyi református egyház anyakönyvébe:
„Híres, nagy elméjű mathematicus volt, az elsők között is első. Kár,
hogy nagy talentuma használatlanul ásatott el.”
Bolyai azonban teljes mértékben tisztában volt saját zsenijével és
munkájának jelentőségével. Hogyan élt ez az ember, honnan származott,
mit tudunk róla, a tudósról és az emberről? A Bolyai-kutatás mára már
világos képet ad számunkra.
A Bolyaiak élete
Bolyai Farkas (1775–1856), János apja is híres matematikus volt, az ő
személyét is számon tartja a nemzetközi matematikatörténet. A
németországi Göttingen patinás egyetemén tanult matematikát 1786–89
között, ahol megismerkedett a matematikusok leendő „fejedelmével”,
Gauss-szal. A két ifjú életreszóló barátságot kötött, mely azonban
elválásuk után csupán levelezésben jutott kifejezésre, személyesen már
nem találkoztak. Farkas taníttatásához a báró Kemény család adta az
anyagi támogatást, tanulótársul vették fiuk, az ifjú báró Kemény Simon
mellé. Ez a továbbtanulási lehetőség akkoriban gyakori volt
tehetséges, de nem jómódú fiatalemberek körében.
A Bolyaiak ősi magyar nemesi család, a Nagyszeben
melletti Bólya nevű településen volt váruk, birtokuk. A családi
hagyomány szerint a Bolyaiak a honfoglaláskor telepedtek le Bólyán (a
település nevét hosszú ó-val, a család nevét röviddel írjuk). A
családdal kapcsolatos első írásos adat a 13. századból származik, a
várkastély tulajdonlásáról szóló legkorábbi írásos emlékek a 16.
századból valók. Egy akkori vitézlő Bolyai János tíz évig volt török
rabságban, birtokai nagy részét elvesztette, a várat is azóta mások
birtokolták, közöttük volt az Arany János által említett Toldi György.
A Bolyai család tulajdonában egy kisbirtok maradt meg Bólyán, Farkas
még itt született. Ehhez járult egy másik kisbirtok Domáldon,
Marosvásárhely mellett, melyet Farkas édesanyja, Pávai Vajna Krisztina
örökölt. Ez akkor került a Bolyai családhoz, amikor Farkas édesapja,
Bolyai Gáspár házasságot kötött, Farkasnak azonban volt egy testvére,
Bolyai Antal, így a domáldi birtokot ketten örökölték. A várkastély
mára már romos, benőtte a gaz, de a háború után még épségben volt,
1960 körül orvosi rendelő működött benne.

Bolyai Farkas arcképe (MTAK Kézirattár)
Bolyai Farkas Erdélybe való hazatérése után
házitanító lett Kolozsvárott. Megnősült, elvette Árkosi Benkő
Zsuzsannát, majd feleségével Domáldra költözött. Fiuk, János születése
előtt felmentek Kolozsvárra, hogy a szülés jobb körülmények között
mehessen végbe. 1804-ben Farkas elnyerte a marosvásárhelyi református
kollégium matematika-, fizika- és kémiaprofesszori állását. A
kollégiumban közép- és felsőfokú oktatás folyt, a felsőfokú oktatók
megkapták a professzori címet. Ezt az állást 1851-ben bekövetkezett
nyugdíjazásáig megtartotta. Felesége 1821-ben meghalt. Öt év múlva
újra megnősült, ám ez a házasság sem volt tartós, a feleség 1833-ban
fiatalon távozott az élők sorából. A második házasságból két gyermek
született, Gergely és Berta, utóbbi azonban már kiskorában meghalt.
Bolyai Farkas főműve a kétkötetes Tentamen
(1832–1833), melyet a kötelező tananyagon túl matematikát tanulni
szándékozó fiatalok számára írt. Valójában a Tentamen a kor
matematikájának magas színvonalú összefoglalása. Bolyai Farkas
foglalkozott még energiatakarékos kályhák készítésével, kertészettel,
erdészettel, drámaírással, színjátszással, zenével, és találmányai is
voltak. A magyaron kívül folyékonyan beszélt németül, latinul,
románul. 1832-ben a Tudós Társaság (a Magyar Tudományos Akadémia
korábbi neve) levelező tagjává választotta, ám nem a Matematikai
Osztályba, székfoglalója pedig egy néprajzi vonatkozású dolgozat volt.
Farkas hosszú időn át kísérletezett az euklideszi 5. posztulátum
bizonyításával, melynek lehetetlenségét éppen saját fia mutatta ki.
Célja elérése érdekében a posztulátum egyenértékű változatait
fogalmazta meg, amivel ő is biztosította helyét a
matematikatörténetben, de voltak egyéb szép eredményei is. 1856.
november 20-án halt meg, sírjára egy általa honosított pojnik almafát
ültettek. Ma is van ott egy pojnik almafa, szorgos kezek ültették
ötven évvel ezelőtt. Temetésekor meghagyása szerint semmi ceremónia
nem volt, csak az oskola csengettyűje szólt.

Bolyai János szülőháza Kolozsvárott, 1903-ban (MTAK
Kézirattár)
Marosvásárhely látképe 1860 körül
(MTAK Kézirattár)

Bolyai Farkas háza Marosvásárhelyen
a lebontás előtt 1909-ben (MTAK Kézirattár)
Bolyai János 1802. december 15-én született
Kolozsvárott, szülőházát emléktábla jelöli. Zsenialitása korán
megnyilvánult. Hatéves korában egyedül tanult meg olvasni, hétévesen
már németül és hegedülni tanult. Apja csak kilencéves korában kezdte
meg rendszeres oktatását, óvakodott attól, hogy fia korai szellemi
fejlődését erőltesse. Kilencéves korától kezdve azonban rendszeresen
tanította, illetve a kollégium legkiválóbb tanulóival taníttatta fiát.
János gyorsan tanult, hamarosan jártasságot szerzett a felsőbb
matematikában. Tizenkét éves korában lett a kollégium rendes
hallgatója, és 1817-ben háromévi kollégiumi tanulás után letette a
rigorózumot. Időközben már felmerült János továbbtanulásának kérdése.
Kézenfekvő volt, hogy Gausshoz, apja barátjához, Göttingenbe menjen
tanulni, s ezalatt Gauss házában lakjon, de ez a terv nem valósult
meg. Farkas 1816-ban Gausshoz intézett kérdezősködő levelére nem
kapott választ. Vannak, akik ezt a levél hangnemének tulajdonítják.
Bolyai Farkas levelei irodalmi remekművek, sok szellemes hasonlatot és
fordulatot tartalmaznak, ez az egy azonban rosszul sikerült. Biztosra
vette, hogy barátja igenlőleg válaszol, és inkább neki voltak
kérdései, hogy elég jó-e fia számára Gauss háza: „Nincs-e lányod, ki
akkor (reciproce) veszedelmessé válhatnék; egészségesek vagytok-e? […]
Feleséged kivétel-e a nők között? Nem változékonyabb, mint a
szélkakas?” Megértjük, hogy erre a levélre Gauss nem reagált. János
Göttingenben való továbbtanulási szándékát az is motiválta, hogy a
pesti és a bécsi egyetemeken akkoriban nem voltak olyan matematikusok,
akiktől sokat tanulhatott volna.
A göttingeni tervek meghiúsulása után János még egy évet
Marosvásárhelyen töltött, közben apja úgy döntött, hogy a Bécsi
Császári és Királyi Hadmérnöki Akadémiára adja fiát. Az ehhez
szükséges anyagiakat gróf Kemény Miklós és mások biztosították. A
sikeres felvételi vizsga után János 1818-ban megkezdte tanulmányait az
akadémián. Öt évet töltött itt. A rendes tanulmányi idő János számára
(akit a negyedik osztályba vettek fel) négy év volt, ám őt, mint az
egyik legjobb tanulót még egy évig további tanulmányokra
visszatartották. Tanárai szerint János volt az évfolyam legjobb
tanulója, diáktársai azonban csak a második helyet juttatták neki a
János által unalmasnak tartott rajzolásban való gyengébb szereplése
miatt. Az összesített eredmény is a második hely lett. Az akadémiai
évek alatt intenzíven foglalkozott matematikával, elsősorban a
párhuzamosok problémájával. Apja azonban óvta ettől, saját magából
kiindulva vélte, hogy fia feleslegesen fecsérli idejét a
megoldhatatlan problémával, és elzárja magát attól, hogy eredményeket
érjen el más vonatkozásban. János, szerencsénkre, nem hallgatott a
figyelmeztető apai szóra, és végül neki sikerült az áttörés, ha az nem
is azzal az eredménnyel zárult, amit az apa elérni remélt.

A bécsi hadmérnöki akadémia épülete
(MTAK Kézirattár)
Jóllehet a hadmérnöki akadémia matematikatanárai
nem tartoztak a kor nagy matematikusai közé, az általuk nyújtott
fegyelmezett oktatás, amely kiterjedt a matematika fizikai és műszaki
alkalmazásaira is, minden bizonnyal hasznára vált Bolyai Jánosnak.
Erről az Appendix és egyéb írásai tanúskodnak. Az Appendix-ben
könnyedén és elegánsan alkalmazza a geometriára az analízis
módszereit, más kézirataiban műszaki problémákat old meg matematikai
módszerrel.

A régi marosvásárhelyi kollégium
(MTAK Kézirattár)
János, miután 1823 szeptemberében megérkezett
Temesvárra, ahová az erődítési igazgatóságra alhadnagyként kinevezték,
még azon év november 3-án apjához intézett levelében tudósít
felfedezéséről. A levél legfontosabb részleteit szinte mindenki
ismeri: „Kedves Édes Apám! Annyi teméntelen meg írni valóm van az ujj
találmányaimról, hogy éppen most nem tudok másként segíteni magamon,
mintha semmibe se ereszkedem belé, tsak egy kvartára írok; […] A
feltételem már áll, hogy mihelyt rendbe szedem, el-készítem, s mód
leszsz, a parallelákról egy munkát adok ki; ebbe a pillanatba nints
kitalálva, de az út mellyen mentem, tsak nem bizonyosan ígérte a tzél
el-érésit, ha az egyébaránt lehetséges; nints meg, de ollyan felséges
dolgokat hoztam ki, hogy magam elbámultam, s örökös kár volna
el-veszni; ha meg-látja Édes Apám meg-esméri; most többet nem
szólhatok, tsak annyit: hogy semmiből egy ujj más világot teremtettem;
mind az, valamint eddig küldöttem, tsak kártyaház a toronyhoz képest.”

Mérnökkari tiszti díszegyenruha
(MTAK Kézirattár)
Bolyai János új világa az abszolút és a
hiperbolikus geometria világa, az első rendszeresen kifejtett
nemeuklideszi geometriáé.
Jánost 1826-ban Aradra helyezték, ahol főnöke az a
Wolter von Eckwehr lett, aki az akadémián számára a matematikát
tanította. Időközben elkészült műve német nyelvű változatával, és azt
Aradon átadta Eckwehrnek. Ez a mű sajnos elveszett. Jánost 1831-ben
Lembergbe helyezték. Odamenet egy kitérővel meglátogatta apját
Marosvásárhelyen, és valószínűleg ekkor adta át neki főműve, az
Appendix kéziratát, ő pedig azt a Tentamen első kötete függelékeként
1832-ben megjelentette, ám különlenyomatként már 1831-ben is kiadta. A
két változat címe lényegtelen különbséget mutat, az 1831-es változat
latin címe: Appendix, Scientiam Spatii absolute veram exhibens; a
veritate aut falsitate Axiomatis XI. Euclidei (a priori haud unquam
decidenda) independentem; adjecta ad casum falsitatis quadratura
circuli geometrica. Magyarul: Appendix, A Tér abszolút igaz Tudománya;
a XI. Eukleidész-féle axióma (a priori soha el nem dönthető) helyes
vagy téves voltától független tárgyalásban; annak téves volta esetére
a kör geometriai négyszögesítésével. A Tentamen második kötete
egyébként 1833-ban jelent meg. Eukleidész művének a Bolyaiak által
ismert kiadásában az 5. posztulátum a XI. jelű.

Az Appendix címlapja Bolyai János kézírásával (MTAK
Kézirattár)
Jánost 1832-ben Olmützbe helyezték, ez volt katonai
pályafutásának utolsó állomása. Egészsége már Aradon megromlott,
megkapta a maláriát, később a kolerát is. Lembergből Olmützbe menet
szekere felborult, és súlyos fejsérülést szenvedett. Matematikával
akart foglalkozni, hogy elméletét továbbfejlessze. Háromévi
szolgálatmentes szabadságot kért János főhercegtől, a hadmérnöki
akadémia főigazgatójától, aki kérvényét elutasította, az ezzel
kapcsolatos szakvélemény egy részletét már idéztük a cikk elején.
Mindamellett másodosztályú kapitánnyá előléptették, de ebben a rangban
1833-ban nyugdíjazták. Olmützbe menet a határon összeszólalkozott a
vámtisztekkel, nem akarván nekik ládáját kinyitni, akik azután
feljelentették. Ez a tény valószínűleg hozzájárult korai
nyugdíjazásához.
János kitűnő hegedűs és vívó volt. Gyakran
játszotta Paganini virtuóz capriccióit. Ami a vívást illeti, egy
valószínűtlen történet szerepel néhány életrajzában. Eszerint Aradon
tizenhárom lovastiszt egyidejűleg párbajra hívta ki hősünket, aki mind
a tizenhárom kihívást elfogadta azzal a feltétellel, hogy a párbajok
között játszhat a hegedűjén. Ha a történet igaz, és a párbajokat
lovassági karddal vívták, amiről köztudott, hogy igen nehéz (több mint
3 kg), akkor ez arra utal, hogy János nagy fizikai erejű fiatalember
volt.
János 1833-ban apjához költözött Marosvásárhelyre.
Egy év múlva kiköltözött Domáldra, ahol 1846-ig lakott, de az újabb
kutatások szerint többnyire inkább Marosvásárhelyen tartózkodott, mert
betegeskedett, és ott gyógyíttatta magát. Együtt élt Kibédi Orbán
Rozáliával. Házasságról eleinte nem lehetett szó, mert a
katonatiszteknél megkövetelt kauciót nem tudta letenni. Az 1848–49-es
forradalom idején eltörölték a kauciót, János és Rozália házasságot
kötött, amit azonban a hadsereg később nem ismert el. A Bolyai család
legjobb ismerője, Oláh-Gál Róbert szerint a kapcsolatból négy gyermek
született: Dénes (1837), Amália (1840), Klára-Eliza (1844) és Gyula
(1855). Dénesnek három házasságából több gyermeke is született, egyes
leszármazottai ma is élnek. Farkas, miután elégedetlen volt János
domáldi gazdálkodásával, a birtokot 1846-ban bérbe adta. Ezt követően
János családjával felköltözött Marosvásárhelyre, ahol házat épített.
Hat év múlva azonban elköltözött családjától, Szőts Júlia nevű
szolgálója gondozta.
A forradalom idején eljutott hozzá az orosz
Nyikolaj Ivanovics Lobacsevszkij műve, melyet szerzője először oroszul
publikált 1829–30-ban, majd németül 1840-ben, és melynek tartalma
közel áll az Appendix-éhez. János előbb gyanakodott, hogy meglopták,
később azonban higgadt fejjel végigolvasta Lobacsevszkij művét, és azt
nagyra értékelte, ám kritikai megjegyzéseket is fűzött hozzá, amelyek
Észrevételek cím alatt találhatók Bolyai kéziratainak jegyzékében.
Bolyai Jánosnak az Appendix mellett egy másik,
régóta ismert tudományos eredménye a komplex számok elméletének
megalapozása, amelyet 1837-ben egy lipcsei pályázatra reagálva foglalt
írásba. A matematikatörténet ezt az eredményt az ír William Rowan
Hamiltonnak tulajdonítja. Bolyai hasonló elveket alkalmazott és
eredményét korábban érte el, mint amikor Hamilton a sajátját a dublini
akadémiához benyújtotta (Bolyai műve már 1831-ben készen volt). A
lipcsei pályázaton egyébként apja is részt vett, de egyikőjük sem
nyert. A teljes díjat nem adták ki, felét odaítélték Kerekes
Ferencnek, a debreceni kollégium tanárának.
Régebben azt tartották, hogy Bolyai János
nyugdíjazása után nem írt már jelentős matematikai művet a Responsio-n
kívül (ez volt a címe lipcsei pályamunkájának). A nemrég elhunyt Kiss
Elemér marosvásárhelyi professzor volt az, aki erre rácáfolt. Gondosan
tanulmányozta Bolyai János háromezer oldalnyi matematikai kéziratát,
és abban olyan „matematikai kincseket” talált, melyek Bolyai idejében
új tudományos eredmények voltak. Egyik számelméleti tételét, mely
egyébként ma tananyag, James Hopwood Jeans angol matematikus
harmincnyolc évvel Bolyai halála után publikálta. A háromezer oldalnyi
kézirat tanulmányozása óriási feladat volt, Bolyai ugyanis nem mindig
rendelkezett megfelelő papírral, feljegyzéseit gyakran arra írta, ami
éppen a keze ügyébe esett: boríték hátlapjára, színlapra, kisfia
teleírt füzetébe stb. A nem matematikai jellegű kéziratokat Benkő Samu
kolozsvári professzor tanulmányozta át nagy gonddal, tizenhat év
munkájával, és írt alapos és szép könyveket Bolyai János
vallomásairól, a két Bolyai kapcsolatáról stb. A nem matematikai
írások, szám szerint kb. 11 ezer oldal, között van az ún. Üdvtan, mely
afféle utópia. Az Üdvtan-nal nem
|
|
|
kívánunk bővebben foglalkozni. Gondolati
tartalmában hasonlít Bolyai János korának egyéb utópisztikus írásaira,
jelentősége azonban nem mérhető az Appendix-éhez.
Marosvásárhelyen János régi és új betegségeivel
küszködve élte magányosan utolsó éveit haláláig, 1860. január 27-ig.
Két nappal később, a temetésen az előírt katonai kíséreten kívül
mindössze két civil jelent meg. Illő dolog tehát, hogy a nemzet lerója
kegyeletét Bolyai János sírjánál, halálának 150. évfordulója
alkalmából.

A két Bolyai síremléke Marosvásárhelyen
A helybéliek nem szereztek tudomást arról, hogy
mit, és milyen jelentőset alkotott Bolyai János. Ám azidőtájt a
szakmán belül sem tudták felmérni annak jelentőségét.
Bolyai Jánosról nem maradt fenn kép. Volt egy, mely
őt katonaruhában ábrázolta, ezt azonban Bolyai egy alkalommal
dührohamában karddal szétkaszabolta. További képek is voltak róla, de
mindegyik megsemmisült. Újabban az a nézet vált elfogadottá (Weszely
Tibor munkássága nyomán), hogy a marosvásárhelyi kultúrpalota
homlokzatának tetején lévő domborművek egyike őt ábrázolja. Az
összesen hat dombormű közül ötnek az esetében sikerült megállapítani,
hogy valóban azokat a személyeket ábrázolják, akiknek a neve a
domborművek alatt olvasható. A hatodik alatt Bolyai János neve áll, és
közvetlenül Bolyai Farkas domborműve mellett helyezkedik el. Van
azonban egyéb bizonyíték is, mégpedig azok tanúságtétele, akik a
kultúrpalota építése idején még éltek és Bolyai Jánost személyesen
ismerték, továbbá az a feltűnő hasonlóság, ami a dombormű és Klapka
György ismert portréja között van. Márpedig jól ismert, hogy Bolyai
János feltűnően hasonlított Klapka György tábornokhoz. Az említett
dombormű felhasználásával készült a 2002. évi Bolyai-évfordulóra,
Széchenyi Kinga Bolyait ábrázoló plakettje.

Bolyai János (Széchenyi Kinga plakettje)
Bolyai János legfontosabb
tudományos eredményei és hatásuk
A deduktív bizonyítás módszere létrejöttének okát tudománytörténészek
a görög demokráciában jelölik meg. A demokrácia ugyanis szükségessé
tette, hogy bírósági tárgyalásokon a pereskedő felek bizonyítsanak, ne
egy tirannus mondja meg, kinek van igaza. Vita van azon, hogy a
matematikusok vagy a filozófusok voltak-e az elsők a deduktív
bizonyítási mód tudományos alkalmazásában, valószínűbb azonban, hogy
inkább az utóbbiak. A deduktív bizonyítást a matematikában Thalész és
Püthagorasz alkalmazta először, a Kr. e. hatodik században,
munkásságuk révén létrejött a deduktív geometria és általában a
deduktív matematika.
Eukleidész, a híres alexandriai matematikus, Platón
iskolájának egykori tanítványa, Kr. e. 300 körül írta Elemek című
művét. Ez tizenhárom könyvből áll, és általános bevezetést nyújt a kor
matematikájába, nem csupán a geometriába. Ennek fényében értjük meg,
hogy Eukleidész a kiinduló alapfeltevéseit két csoportba sorolta:
követelmények és közönséges ismeretek. Az első csoport kifejezetten
geometriai állításokat tartalmaz, a második csoportban azonban
általánosabb érvényű állítások foglalnak helyet. Az előbbieket
latinosan posztulátumoknak is nevezzük, az utóbbiakat későbbi
kommentátorok axiómáknak nevezték el. (Az axióma szót Eukleidész nem
használta, de Arisztotelész óta ismert volt a görög filozófiában.)
Elfogadottá vált az a felfogás, hogy az axióma nyilvánvaló igazságot
fejez ki, a posztulátum pedig általunk bevezetett feltételezés. (Ma
már nem teszünk különbséget közöttük, és bármilyen matematikai elmélet
kiinduló állításait axiómáknak nevezzük.) Eukleidész posztulátumai
előírják például, hogy két pont meghatároz egy egyenest, a derékszögek
egyenlők stb. Az 5. posztulátum azonban olyan állítást tartalmaz,
amely nem szemléletes, mert nem tudunk egyeneseket végtelenbe menően
követni. Ez eredeti formájában a következő: ha egy egyenes metsz két
egyenest és az azonos oldalon lévő belső szögek összege kisebb két
derékszögnél, akkor a két egyenes a végtelenségig meghosszabbítva
metszi egymást azon az oldalon, amelyen a szögösszeg kisebb két
derékszögnél. Ezzel egyenértékű az az állítás, hogy adott egyeneshez
egy rajta kívül fekvő ponton át egy és csakis egy olyan egyenes
húzható, mely nem metszi az adott egyenest, továbbá egyenértékű az is,
hogy a háromszög szögeinek összege 180º. Kérdés: bebizonyítható-e az
5. posztulátum Eukleidész egyéb posztulátumára és axiómáira
támaszkodva? A több mint kétezer éves problémára a választ a magyar
Bolyai János és az orosz Nyikolaj Ivanovics Lobacsevszkij adta meg: az
5. posztulátum független a többitől. Annak elvetése esetén új
geometriákat kapunk, mégpedig, ha legalább két nem metsző egyenes
húzható, akkor a Bolyai–Lobocsevszkij-féle (más szóhasználattal:
hiberbolikus) geometriát, ha pedig egy sincs, akkor az elliptikus
geometriát kapjuk. Ilyen például a gömbi geometria, ha egyeneseknek az
ún. főköröket tekintjük.
Bolyai továbbment, és kiépítette az ún. abszolút
geometriát is; ez olyan állításokat tartalmaz, melyek az 5.
posztulátum elvetése vagy előírása esetén egyaránt érvényesek. Az
alábbiakban ízelítőül felvázolunk néhány tételt a Bolyai-geometriából.
Vegyünk fel a síkban egy l egyenest, egy rajta
kívül fekvő P pontot, majd egy arra illeszkedő olyan egyenest, mely
l-et metszi. Az utóbbi egyenes elforgatása során előáll egy olyan
helyzet, hogy a P pontra illeszkedő egyenesünk „elpattan” l-től, annak
egyik oldalán. A másik irányba való forgatáskor egy másik elpattanó
egyenes adódik. Bolyai meghatározta az ábrán látható α szög és a
hiperbolikus geometriai d távolság közötti kapcsolatot, melyet az
alábbi formulával adott meg:
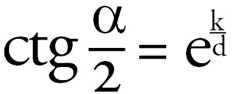
A formulában szereplő k állandó univerzális,
független attól, hogy mely l egyenest és P pontot vesszük. Ugyanez a k
fordul elő más geometriai mérőszámok képletében is Bolyai
geometriájában.
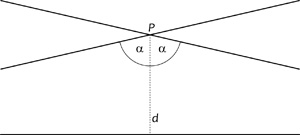
Elpattanó egyenesek
Bolyai kiépítette az abszolút és a hiperbolikus
geometria trigonometriáját, és alkalmazta az ívhossz, a felszín és a
köbtartalom meghatározására. Például az r sugarú kör kerülete a
hiperbolikus geometriában az alábbi értékkel egyenlő:
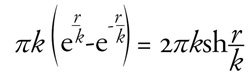
ahol k a már ismert, az egész térre nézve univerzális állandó. Ezt a
későbbi matematikai művekben a tér görbületének reciprokával
azonosították. Ha k → ∞, akkor a fenti formula határeseteként 2rπ
adódik, ami a kör kerületének jól ismert képlete az euklideszi
geometriában. (Az sh a szinuszhiperbolikusz függvény rövidítése,
jelentése a formulából kiolvasható; lentebb szerepel a ch szimbólum,
ez a koszinuszhiperbolikusz függvényt jelöli, mely az előbbitől abban
különbözik, hogy mínusz helyett plusz áll a képletben.)
Bolyai János egyik legszebb, az abszolút
geometriában érvényes tétele az alábbi. Egy háromszög szögeinek
szinuszai úgy aránylanak egymáshoz, mint azoknak a köröknek a
kerületei, amelyeknek sugarai rendre megegyeznek a szemben lévő
oldalakkal. Ha a szögeket A, B, C, a szemben lévő oldalakat a,b,c, az
r sugarú kör kerületét οr jelöli, akkor tehát Bolyai tétele a
οa : οb : οc = sin A: sin B: sin C
formulával fejezhető ki. Az euklideszi geometriában
οr = 2πr, a fenti formula tehát az ismert a : b : c = sinA : sinB :
sinC alakot ölti. A hiperbolikus geometria esetében viszont
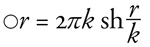
amiből következik, hogy
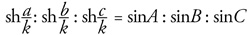
Ha egy háromszög szögei α, β, γ, akkor az euklideszi geometriában
α+β+γ=π, a hiperbolikus geometriában azonban α+β+γ<π. A két szám
π-(α+β+γ) különbségét a háromszög defektusának nevezzük. Bolyai
bebizonyította, hogy a háromszög ∆ területe egyenlő az alábbi
mennyiséggel:
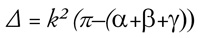
ahol k a korábbról ismert univerzális állandó. Ezt a formulát Johann
Heinrich Lambert, a nemeuklideszi geometria előfutára is ismerte,
Bolyai viszont szabatosan bebizonyította.
A hiperbolikus geometriában egy derékszögű háromszög a, b befogóira és
c átfogójára (a szög az „egyenesek” metszéspontjában található szöget
jelenti) érvényes az alábbi formula:
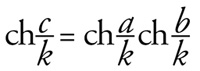
Ha k → ∞, akkor határesetként a c²=a²+b² formulát kapjuk, ami
Pitagorasz tételét jelenti.
Bolyai János munkája nagyban hozzájárult ahhoz,
hogy a geometria, melynek korábban természettudományi jellege volt,
önálló, elvont matematikai struktúrák tudományává vált. Ám éppen ez
segítette hozzá, hogy széleskörű alkalmazást nyerjen, ne csak közeli
fizikai világunk térformáit írjuk le geometriai fogalmakkal. A
„folytonos” nemeuklideszi geometriákon kívül létrejöttek a „diszkrét”
és a „véges” geometriák, az utóbbiakat alkalmazzák a kódolás
elméletében, kísérletek tervezésében stb. Az axiomatikus módszer a
matematika minden ágába bevonult, és a matematika átalakulását
eredményezte. Az euklideszi geometria egyeduralmának megtörése utat
nyitott a huszadik század modern fizikai elméletei számára.
Az axiomatikus gondolkodásmód a számítógépes
alkalmazásban is meghonosodott a matematikai modellek alkalmazása
révén. Amikor egy gyakorlati problémát megoldunk – ma már általában
számítógép segítségével –, akkor feltevéseinket rendszerbe foglaljuk,
minden ilyen rendszer egy axiómarendszer, majd a számítógéppel
elvégeztetjük a feladatmegoldáshoz szükséges számításokat.
Bolyai és Lobacsevszkij eredménye a nem szakember
számára ma is érthetetlennek tűnhet. Ugyanis a gyakorlati életben,
környezetünk véges világában számtalan esetben alkalmazunk az 5.
posztulátumra emlékeztető elvet, például földmérés során,
tervezőmunkában, nem is kell, hogy törődjünk egyéb lehetőséggel, adott
egyeneshez egy rajta kívül fekvő ponton át egy és csak egy párhuzamos
egyenes szakaszt tudunk megrajzolni. Ha nem is lehet az 5.
posztulátumot a többi állításból levezetni, érvelhetne valaki, a világ
akkor is az euklideszi geometriát követi. Bolyai és Lobacsevszkij
idejében mindenesetre ez volt a meggyőződés, és ezt minden idők egyik
legnagyobb filozófusára, Immanuel Kantra való hivatkozással is
alátámasztották. Mindezeket figyelembe véve megértjük, hogy a
matematikusok körében megoszlottak a vélemények az új geometria
jelentőségét illetően. Ámde nemcsak a matematikusokra kellett
figyelni. Elterjedt vélemény sokak körében ma is, hogy Gauss
birtokában volt az új geometriának, de nem merte azt közzétenni.
Hagyatékában nem találtak erre vonatkozó bizonyítékot, de érdemes
foglalkozni azzal, hogy vajon miért gondolták és gondolják ma is, hogy
Gauss félt a nemeuklideszi eredményeket publikálni? Különös dolog
félni igaz matematikai tételek közzétételétől, kiváltképp, ha az, aki
fél, a történelem egyik legnagyobb matematikusa, és nemcsak mint
egyetemi tanár, hanem mint közéleti személyiség is nagytekintélyű, a
hannoveri királyság udvari tanácsosa, Herr Hofrat. Ez a megszólítás
illette meg Gausst tudományos körökben is. A fentiek arra utalnak,
hogy a nemeuklideszi geometria felfedezésének jelentősége túlmegy a
matematikán. Valóban, az új geometria és annak későbbi kiterjesztései
átalakították a matematikát és fizikai világképünket. Érdekes
fejlemény: a geometria megszűnt természettudomány lenni, viszont az
egyik legfontosabb természettudomány, a fizika számára ezáltal nyílt
meg a geometrizálódás útja. Ám a Bolyai-geometria nemcsak a
matematikára és fizikai világképünkre, hanem az emberi gondolkodásra
is hatással volt. Megtudtuk, hogy van olyan zárt gondolati rendszer,
melyben van eldönthetetlen probléma, nem is akármilyen, hanem olyan,
ami kétezer év óta foglalkoztatta a legkiválóbb elméket. Egy másik,
axiómarendszereken belül eldönthetetlen problémára vonatkozó példa a
halmazelmélet keretében keletkezett a 20. században.
Az osztrák származású Kurt Gödel pedig megmutatta,
hogy az axiomatikus rendszerekben mindig vannak megoldhatatlan
problémák, a triviális esetektől eltekintve.
Ennek a nagyszabású mozgalomnak a Bolyai-geometria
megalkotása volt a kiindulópontja. Morris Kline amerikai
matematikatörténész azt írta összefoglaló monumentális művében, hogy
az ókori görögök óta nem volt olyan nagy forradalom a matematikában,
mint a nemeuklideszi geometria felfedezése. Hozzátehetjük: a logikában
sem, Arisztotelész óta. Még távol vagyunk attól, hogy ismernénk akár
nagy vonalaiban a nemeuklideszi geometria felfedezésének
kultúrtörténeti hatását, a kutatómunka azonban elindult, és várhatóan
sok fontos és érdekes eredményt fog hozni a közeli jövőben.
A modern fizikai elméletek jelentős része
nemeuklideszi geometrián alapul. Az elméletek egy részét kísérletileg
is alátámasztották, naprendszeri méretekben a tér nemeuklideszinek
bizonyul. A legfrissebb kutatási eredmények szerint kozmikus
méretekben azonban mégis jó közelítést nyújt az euklideszi geometria.
Ugyanis a tér görbületét a tömeg jelenlétének tulajdonítjuk, a
kozmoszban pedig az anyagsűrűség kicsi.
Publikáció és utóhatás
A tudományos eredményeket nem elég elérni, azokat széles körben meg
kell ismertetni, ám ehhez jó publikálási lehetőségek kellenek, amik
sem Erdélyben, sem Magyarországon akkoriban nem voltak. Bolyai Farkas
azt javasolta fiának, hogy eredményeit a Tentamen appendixeként
publikálja. Az apa ezt jó érzékkel tette, mert egyfelől, amint fiához
írja: „…félős, hogy más is kifejti és hamarább kiadja, mivel a
dolgoknak meg van a maguk korszaka”, másfelől azonban, úgy tűnik, nem
is nagyon volt más lehetőség. A marosvásárhelyi kollégiumi tankönyv
függelékeként publikált Bolyai-mű nem számíthatott arra, hogy a kor
tudósai felfigyelnek rá. Volt azonban valaki, éppenséggel a kor és
minden idők egyik legnagyobb matematikusa, a híres göttingeni
professzor, Bolyai Farkas fiatalkori barátja: Gauss, aki tudomást
szerzett az Appendix-ről. Ugyanis Farkas elküldte neki az 1831-ben
különlenyomatként megjelent művet.
Az első, 1831 júniusában postán feladott példány
elveszett. A második példányt az ifjú báró Zeyk József személyesen
vitte el a híres tudóshoz. Gauss az Appendix kézhezvételekor azt
mondta: „nagyra törsz Phaithón” (Phaithón a görög mitológiában a Nap
fia, aki elbizakodottságában kormányozni akarja apja szekerét). Gauss
mégis kedvezőtlen levelet írt Bolyai Farkasnak. Amint az 1832. március
6-án keltezett levélből már idéztük, azt állította, hogy a benne
foglalt eredmények megegyeznek harminc-harmincöt éve folytatott
meditációjával. Ám Gauss 1855-ben bekövetkezett halála után
hagyatékában nem találtak olyan kéziratokat, melyek állítását
alátámasztanák. A levél Jánost mélyen lesújtotta. Gauss magatartása
még inkább bírálható, ha figyelembe vesszük, mit írt néhány héttel
korábban, február 14-én, a marburgi professzor Gerlingnek: „Ezt a
fiatal geométert, Bolyait, elsőrangú lángésznek tartom”. Ha ezt a
Bolyaiaknak is megírja, bizonyára másként alakult volna János élete.
János azonban apján kívül mástól nem kapott elismerést. Lipcsei
pályázatát sem koronázta siker. Nem lett tagja a Tudós Társaságnak,
bár a Bolyaiakat ismerő Döbrentei Gábor titoknok foglalkozott ennek
lehetőségével. Úgy gondolta, hogy a deák nyelven írt Appendix nem
teszi ezt lehetővé, minthogy a Tudós Társaság a magyar nyelv
művelésére alapíttatott. A Tudós Társaság Matematikai Osztályán
azonban Bolyai János művét nem méltányolták, talán nem is ismerték. Ez
abból tűnik ki, hogy Vállas Antal matematikus akadémikus 1836-ban
összefoglaló cikket közölt az akkori és a korábbi magyar matematikusok
tudományos eredményeiről. Ebben Bolyai Farkas szerepel (előnytelen
beállításban), de János nem. Vállas hosszasan magyarázza a
bizonyítványunkat, hogy miért nem tudtunk nagyot alkotni, itt volt a
tatár, a török stb. Közben pedig a világraszóló új tudományos
eredményt tartalmazó Appendix már ott volt a Tudós Társaság
könyvtárában, ahová azt Bolyai Farkas 1832-ben megküldte, saját
művével a Tentamen-nel együtt.
Az Appendix-re a kor matematikusai akkor figyeltek
fel, amikor Gauss halála után hagyatékát feldolgozták. Ezt követően
külföldön felgyorsultak az események. 1868-ban egy befolyásos német
tankönyv (szerzője Richard Baltzer) már említi Bolyai eredményeit.
Ekkoriban lépett színre a francia Guillaume Jules Hoüel, a
matematikatörténet professzora Bordeaux egyetemén. Franciára
fordította az Appendix-et, és mellékelte a magyarországi kapcsolata,
Schmidt Ferenc temesvári építész által készített, a Bolyaiakról szóló
életrajzot. Bolyai János elismertetése azonban vontatottan haladt,
miközben a tudományos világ már ünnepelte Lobacsevszkijt. Hoüel
szeretett volna információt kapni a Marosvásárhelyen ládákban
szunnyadó Bolyai-kéziratokról. Levelet írt Marosvásárhelyre, válasz
nem érkezett. Schmidt Ferencet mozgósította, ő sem járt eredménnyel.
Időközben tudomására jutott, hogy Olaszországban olaszra fordították
az Appendix-et, és az abban foglaltakat Rómában igen nagyra
értékelték. Felkérte hát Balthasar Boncompagni herceget, a Római
Akadémia tagját, tudománytörténészt, hogy ő írjon levelet báró Eötvös
Józsefnek, aki akkor a Magyar Tudományos Akadémia elnöke és
kultuszminiszter volt egy személyben. A levélben segítséget kér
Eötvöstől ahhoz, hogy kapcsolatot létesítsen a marosvásárhelyiekkel
Bolyai Jánosra vonatkozó információk szerzése céljából. Eötvös ezt
követően azt írta fiának, Lorándnak, hogy nem tudja, örüljünk vagy
piruljunk, majd tekintélyét latba vetette, és a Bolyai-ládák 1869-ben
felkerültek az Akadémia könyvtárába átvizsgálás céljából, hogy ti.
van-e a kéziratokban további jelentős tudományos eredmény (a
kéziratokat János halála után helyezték ládákba, ma a marosvásárhelyi
Teleki Tékában harmincöt vastag dossziét töltenek meg). A munka lassan
haladt, végül egy levélen kívül, melyben János hírt adott apjának
arról, hogy „a semmiből egy ujj más világot teremtettem”, az
átvizsgálásra kiküldött bizottság érdemlegeset nem talált. A ládák
1894-ben visszakerültek Marosvásárhelyre. A hagyatékban szunnyadó
matematikai írások egy részének átvizsgálására a 19. század végén sor
került ugyan, a továbbiakkal, mint említettük, majdnem teljes körűen
csak mostanában, száz évvel később történt meg ez.
Talán más lett volna a helyzet, ha Eötvös József
nem halt volna meg 1871-ben, és még néhány évig szorgalmazta volna a
Bolyai-kutatást. Eötvös egyénisége, nemzetközi elismertsége (könyvei
németül, angolul is megjelentek) kellő alapot szolgáltatott volna
Bolyai János nemzetközi elismertetéséhez is. Ez végül lassan megindult
ugyan, főként a francia Hoüel és a német Paul Stäckel
matematikatörténészek munkássága révén, ám külföldön Bolyai mind a mai
napig gyakran háttérbe szorul Lobacsevszkij és Gauss mögött.
Hozzájárul ehhez az is, hogy Bolyai Jánosról angol nyelven nincs elég
széleskörű irodalom.
Száz évvel ezelőtt a Magyar Tudományos Akadémia
megalapította a nemzetközi Bolyai-díjat. Ezt 1905-ben a francia Henri
Poincaré, 1910-ben a német David Hilbert kapta meg. Mindketten igen
fontos eredményeket értek el a geometria területén. A díj segítette
Bolyai János jobb nemzetközi elismertetését, kiosztása azonban
megszakadt. Néhány évvel ezelőtt az Akadémia a díjat felújította, és
két alkalommal ki is adta. Az izraeli Saharon Shelah kapta meg
2000-ben és az orosz Misa (Mihail Leonyidovics) Gromov 2005-ben. Idén
megint esedékes a díj kiadása.
Bolyai János a magyar tudomány legnagyobb és a
nemzetközi tudomány kiemelkedő alakja. Megoldott egy kétezer éves
matematikai problémát; ennek hatására elsősorban a geometria, de a
matematika egyéb fejezetei is átalakultak; lehetővé tette, hogy a
térről másként gondolkodjunk, és ezzel utat nyitott a huszadik század
modern fizikai elméletei számára; megmutatta, hogy van olyan probléma,
mely adott axiómarendszeren belül nem dönthető el, és ezzel jelentősen
hozzájárult a logika és általában az emberi gondolkodás fejlődéséhez.
Minthogy a modern, számítógépes alkalmazott matematikai
feladatmegoldás is axiómarendszerek révén történik, Bolyai hatása
közvetve ebben is megnyilvánul.
Az Appendix-nek a Magyar Tudományos Akadémia
Könyvtára Kézirattárában lévő eredeti példányát 2009-ben az UNESCO
felvette a Világemlékezet Listájára.
Legyünk büszkék nemzetünk nagy fiára, és ápoljuk
kultuszát. Halálának 150. évfordulóján pedig zarándokoljunk el
marosvásárhelyi sírjához, hogy lerójuk kegyeletünket a sokat
szenvedett nagy tudós iránt, és gyarapítsuk életével, alkotásával
kapcsolatos ismereteinket.
Kulcsszavak: Bolyai János, Appendix, Bolyai Farkas, Tentamen,
nemeuklideszi geometria, hiperbolikus geometria, abszolút geometria,
axiomatikus módszer, matematikatörténet, kultúrtörténet
IRODALOM
Alexits György (1977): Bolyai János
világa. Akadémiai, Budapest
Ács Tibor (2004): Bolyai János új
arca – a hadmérnök. Akadémiai, Budapest
Benkő Samu (1968): Bolyai János
vallomásai. Irodalmi, Bukarest
Bolyai Farkas (1832–1833): Tentamen.
Maros Vásárhely, 2. kiadás:
WEBCÍM >
Dávid Lajos (1979): A két Bolyai
élete és munkássága. Második kiadás. Gondolat, Budapest
Kiss Elemér (1999): Matematikai
kincsek Bolyai János hagyatékából. Akadémiai, Budapest
Oláh-Gál Róbert (2009): Erdélyi
tájakon a Bolyaiak nyomában. Pro-Print Kiadó, Csíkszereda
Prékopa András (2003): Bolyai János
forradalma. Természet Világa. 134, 3–21.
Szénássy Barna (1970): A
magyarországi matematika története a 20. század elejéig. Akadémiai,
Budapest
Weszely Tibor (2002): Bolyai János.
Az első 200 év. Vince, Budapest
LÁBJEGYZET
* A Bolyai János
Emlékkonferencia megnyitó ülésén, 2010. augusztus 30-án, a Magyar
Tudományos Akadémián elhangzott előadás szerkesztett változata.
<
|
|