Simonyi Károly az ajándékot, amelyet olvasóinak készített, gondosan becsomagolta. Nyilván meg akart lepni bennünket. A könyv fülszövege − idézet Staar Gyula nagyszerű interjúkötetéből − igencsak szerényen hangzik. A szerző korábbi egyetemi előadásaira emlékszik: „A lankadó figyelem élénkítésére, pihentetésre én történelmi anekdotákat, verseket mondtam. Ezek mindig kapcsolatban álltak a konkrét szakmai mondanivalómmal. Pontosan emlékszem arra az időre, amikor elhatároztam, hogy ebből a »lazításból« könyv lesz, megírom a fizika kultúrtörténetét.” Ennyi lenne tehát ez a munka? Anekdotafüzér és szép idézetek gyűjteménye?

Az első fejezet ennél már magasabbra teszi a mércét. C. P. Snow könyvéből, A két kultúrából idéz: „Azt hiszem, hogy a nyugati társadalom egészének intellektuális élete egyre növekvő mértékben hasad szét két szemben álló csoportra […] az irodalmárok az egyik oldalon, a tudósok – és ezek között is elsősorban a fizikusok – a másikon.” A tétel illusztrálására Snow azt az őt elrettentő tapasztalatát idézi fel, hogy művelt íróemberek társaságában senki nem tudta, micsoda a termodinamika második főtétele. Olyan ez – írja – , mintha egy fizikus semmit se tudna Shakespeare-ről! A tapasztalat szomorú valóban, de nem hiszem, hogy A fizika kultúrtörténete ennek a dichotómiának lenne az orvossága. Nem ezért írták!

A tudománytörténész, George Sarton írta egyszer, egyebek mellett nyilván saját területének az igazolására is, hogy „a tudománytörténet jelenti az egyetlen hidat a természettudományok és a humaniórák között”. Ez bizonyára igaz is, lényeges is. De Simonyi könyve nem a fizika tudományának a története, amely kitekint a humaniórákra. A könyv az emberi kultúra története, amelynek tengelyébe a szerző a fizikai megismerést helyezi.

Nézzük például Quentin de la Tour festményét, a Mme. Pompadourt ábrázoló szép portrét! Az előkelő gazdagságot sugalló környezetben Simonyi észreveszi a hölgy melletti asztalon álló könyveket – a Nagy Enciklopédia köteteit. A királyi szerető, aki bizonnyal nem pusztán szellemi kiválóságának köszönhette fejedelmi pályafutását, gondot fordított arra is, hogy korszerűen művelt asszonynak tekintsék; ezt a felvilágosodás korának nagy művével akarta demonstrálni. A francia arisztokrácia világát, egy egész korszak szellemi szerkezetét állítja elénk a kép – a képaláírás még a közelítő forradalmat is megidézi.

A korszak a fizikának is nagy ideje. A mechanika alapjait Isaac Newton már egy évszázaddal korábban lefektette, a természettudományos gondolkodás módját, ha implicit módon is, meghatározta. Ezek hatása megfellebbezhetetlennek látszott – az ő eredményeit és módszereit próbálták meg alkalmazni a tudomány minden területén. A hő jelenségeinek a vizsgálata sem volt kivétel. A XVIII. század második felétől meginduló fejlődést, amely az elemi fogalmak tisztázásával kezdődött, majd a hő- és mechanikai energia egyenértékűségének felismerésével, tehát az energiamegmaradás elvének kimondásával tetőzött, Simonyi egy folyamatábrán szemlélteti (1. ábra).

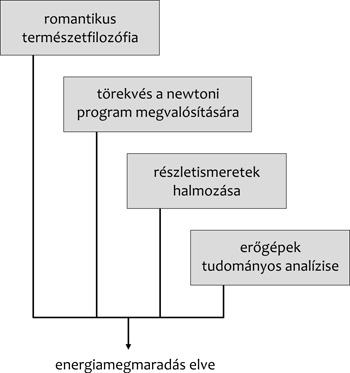
1. ábra

Romantikus természetfilozófiáról szólva elsősorban talán Friedrich Schellingre gondolt, akiről a könyv egy másik helyén azt írja, filozófiájában az összes természeti jelenséget egyetlen ősprincípium megjelenési formájának tekintette. Ez a szemlélet, amely korának romantikus költészetéből is táplálkozhatott, sok fizikus gondolkodását szabadította ki a naiv, mechanikus materializmus korlátai közül.

A newtoni program megvalósításán két törekvést is érthetünk. Egyfelől a jelenségek matematikailag szabatos leírását akarja elérni, másfelől tömeggel bíró anyagi részek viselkedésén alapuló, szemléletes modelleket kíván alkotni. Ez a két igény a hőjelenségek világában hosszú időn át kizárta egymást.

Első lépés a mérhető mennyiségek értelmezése, fogalmi meghatározása volt. Angliában Joseph Black, Franciaországban Antoine Lavoisier és Pierre-Simon Laplace kísérletei vezettek el hő és hőmérséklet megkülönböztetéséhez, a fázisátmeneteket kiváltó látens hő megfigyeléséhez. Egyik legfontosabb eredményük annak a felismerése volt, hogy izolált rendszerekben a hő megmarad. A melegebb edényből a hidegebbe veszteség nélkül lehet átvinni a hőt – akárcsak valami folyadékot. Ez alapvetőnek bizonyult. Két megmaradó mennyiséget ismertek abban a korban: a tömeget, és az „eleven erőt”, mai nevén a kinetikus energiát. A hő tehát lehet anyag, és lehet kinetikus energia, a két lehetőség fenomenologikusan egyenértékűnek látszott.

Azt, hogy a hő a mozgással áll kapcsolatban, már korábban is sokan gyanították: Francis Bacon egyszerű megfigyelések alapján, Leonhard Euler és Gottfried Wilhelm Leibniz a súrlódással vagy rugalmatlan ütközésekkel kapcsolatos hőmérséklet-emelkedést értelmezve jutott arra a következtetésre, hogy a hő – mozgási energia. A döntő, „majdnem” kvantitatív bizonyítékot Rumford gróf (Benjamin Thompson) ágyúfúrási kísérletei szolgáltatták. Tompa hegyű fúróval fúrt ágyúcsöveket, és azt tapasztalta, hogy a cső hőmérséklete megemelkedett anélkül, hogy anyagában bármi szemmel látható változást szenvedett volna. Megmérte a felmelegedett ágyúcső tömegét is, és semmilyen mérhető tömegnövekedést nem tapasztalt. Ha a hő tömeggel bíró anyagi fluidum, akkoriban használt nevén caloricum volna, úgy áramlását tömegváltozásnak kellene kísérnie.

Mindez erős érv lehetett az energetikai értelmezés mellett, összhangban is állt a mechanikai modellel szemben támasztott igényekkel. A kor ismereteinek szintjén azonban alkalmatlan volt arra, hogy kvantitatív elmélet, analitikusan tárgyalható leírás alapja lehessen. Erre a caloricummodell megfelelőbbnek bizonyult. Simonyi táblázatban foglalta össze a két modell teljesítőképességét (2. ábra).

Úgy tanultuk, Nicolas Carnot-nak a hőerőgépek hatásfokára irányuló vizsgálatai vezettek el a termodinamika II. főtételéhez, a termikus folyamatok irreverzibilitásának kimondásához. Most megtanulhatjuk, hogy ez csak erős megszorításokkal igaz. Carnot ugyanis úgy gondolta, hogy a Q mennyiségű caloricum a magasabb T₂ hőmérsékletről lefolyik az alacsonyabb T₁ hőmérsékletre, a mennyisége azonban megmarad. Ezért a hatásfokot így kell kiszámítanunk:

η = Q(T₂-T₁)/QT₂ = 1 – T₁/T₂.

Carnot ugyanis a lefolyó víz és az áramló hő munkavégzése között tökéletes analógiát tételezett fel, épp olyat, amilyenre később az elektromos áram munkája kapcsán gondoltak. Ahogyan a víz állandó M tömege azért végez munkát, mert a nehézségi erő irányában áramlik, vagy az állandó mennyiségű elektromos töltés azért, mert a csökkenő elektromos potenciál felé mozdul el, úgy áramlik az állandó mennyiségű caloricum a melegebb helyről a hidegebb felé. De hát ez nincsen így – a helyes viszonyokat a 3. ábra mutatja. A termodinamika szerint a hő nem marad meg, ha munkavégzésre fogjuk. A hatásfok helyes, a főtételeken alapuló kifejezése:

η= (Q₂ - Q)₁/Q₂ ,

amit egyesítve hő és hőmérséklet arányosságával, Q₁/Q₂ = T₁/T₂, eljutunk Carnot fent írt kifejezéséhez. Vagyis Carnot helytelen elgondolás alapján, a caloricumelmélet tévedését alkalmazva jutott helyes, tapasztalatilag igazolható eredményre. Ez a tévedés fontos érv volt a caloricummodell mellett.

Talán ennél is többet nyomott a latban Joseph Fourier hővezetési elmélete. Legegyszerűbb formájában ez egy állandó keresztmetszetű szilárd rúdban, a rúd tengelye mentén kialakuló hőmérséklet-eloszlásra vonatkozik, ha a rúd két

végének hőmérséklete eltér egymástól. A hőátadás sebességére: a hőáramra, tehát a dQ/dt deriváltra egy tapasztalati, konstitutív egyenletet írt fel:

dQ/dt = - κ∂T/∂x

.

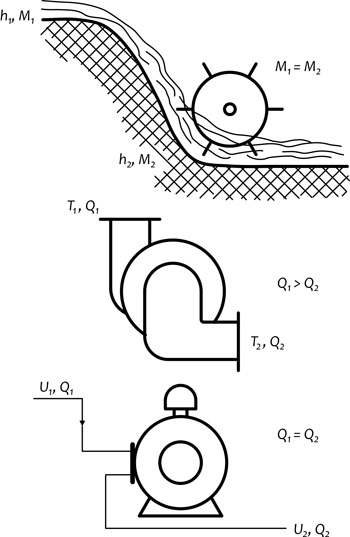
3. ábra

A kifejezés szépen értelmezhető a hőmérsékletesés mentén áramló caloricum elképzelésével. Ezt a hő megmaradásának tételével egyesítve jutott a hővezetés differenciálegyenletéhez (itt c a fajhő, r a sűrűség jele):

∂T/∂t= κ/cρ ∙ ∂²T/∂x².

Az egyenlet megoldásait keresve alkotta meg a Fourier-sorok módszerét is. A differenciálegyenlet megoldásai teljes általánosságban és nagy pontossággal adják meg a hőmérséklet-eloszlásokat, a legkülönfélébb feltételek mellett. Ez az eredmény is a caloricumelképzelés mellett szólt.

A súrlódásból keletkező hő jelenségére azonban ez a modell nem adott választ. Később, abban a korszakban, amelyben egyfelől az anyag diszkontinuus felépítését egyre komolyabban kellett venni, amikor, Simonyi szavával, a kémia lett az anyag atomos szerkezetének propagálója, másfelől amikor Julius R. Mayer, majd James Joule nyomán világossá vált, hogy a hő pusztán egy fajtája az energiának, hozzá kellett fogni a kinetikus modell matematikai leírásához.

James C. Maxwell az alkalmazott mechanika egy érdekes példájaként számította ki a gázok részecskéinek egyensúlyi sebességeloszlását. Ludwig Boltzmann-nak a részecskék sebességére vonatkozó mérlegegyenlete a kis nyomású gázokban lejátszódó transzportfolyamatokról is számot tudott adni. Ennek a fejlődésnek a csúcspontja talán az úgynevezett H-teoréma kidolgozása volt. A következőről van szó.Legyen f(v)dv annak a valószínűsége, hogy egy részecske sebessége v és v+dv közé esik. Boltzman úgy találta, hogy az alábbi, H-val jelölt integrál

H = ∫f(v)lnf(v)dv

az idő előrehaladtával monoton csökken egy határérték felé. A határérték pedig az entrópia (-1)-szeresével arányos:

lim H ~ -S

t→∞

Ez nagyon fontos eredmény volt – a kinetikus modell, úgy látszott, értelmezni tudja a termodinamikai folyamatok időbeli lefolyását, azt például, hogy a hő mindig a melegebb helyről áramlik a hidegebb felé. Ezt az egyirányúságot fejezi ki matematikailag a Rudolf Clausius bevezette entrópiafüggvény is; ez eredeti megfogalmazásában csak makroszkóposan megfigyelhető mennyiségek – hő, hőmérséklet, nyomás, térfogat, koncentráció – ismeretét igényelte, ezek mikrofizikai (atomi-molekuláris) magyarázatára nem tért ki. A H-teoréma úgy látszott, értelmezni tudja az entrópia növekedését a részecskék ütközésének a szintjén.

Ez azonban csak igen korlátozottan, egy speciális modell keretein belül igaz. A részecskék csak tökéletesen rugalmasan ütközhetnek egymással, kizárólag páros ütközések fordulhatnak elő, és két ütközés között semmilyen korreláció nem állhat fenn – az ütköző részecskék felejtsék el a múltjukat. Mindmáig nem sikerült általánosítani a H-teorémát, ebben az értelemben a mikrofizikai modell ma is adósa a makroszkópos termodinamikának.

Ám Boltzmann tovább gondolkodott. Simonyi idézi kijelentését: „A hő mechanikai elméletének problémái egyúttal a valószínűségelmélet problémái is.” Bevezette a termodinamikai valószínűség fogalmát, s ennek logaritmusát arányosnak tekintette az entrópiával:

S = klnW.

(A k együttható mindmáig Boltzmann nevét viseli.) Az entrópia növekedése tehát a valószínűség növekedését jelenti. Az azonban, hogy a valószínűség nő, nem következik a valószínűség-számítás semelyik tételéből. Ez független, az entrópia növekedésének tételével egyenértékű kijelentés. Simonyi a könyv egy más helyén igen tömören összefoglalja a kanti filozófiából azt, amiről úgy tartotta, érdekes és értékes lehet a fizikusnak. Itt ír a korábbi ismeretekből nem következő, a priori szintetikus ítéletekről; igazából ezek viszik előre a tudományt. Azt hiszem, a fenti összefüggést ilyen ítéletnek kell tartanunk.

Az entrópianövekedés tételéből jutott Clausius a hőhalál eszméjére: mivel minden energiafajta végül hővé alakul, a világegyetem hőmérséklete minden határon túl növekszik, elpusztul a világ. A korszak, a XIX. század vége hajlamos volt az ilyenfajta pesszimizmusra, készségesen befogadta ezt az eszmét. A könyvben egy francia szimbolista költő, Jules Laforgue egy versét olvashatjuk, amely címe és tartalma szerint Gyászinduló a Föld halálára. Egy versszakot írok csak ide belőle, Kálnoky László fordításában:

Ó, gyászkísérete Pazar fényű Napoknak,

hullámozz, kavarogj aranyszínű tömeg,

holt húgotok mögött, kit most temetni fognak,

lassan, búsan, komor zenére lépjetek.

Nem az entrópiatörvénytől lett gyászos a költő, nem a verstől a fizikus. Ilyen volt az egész korszak.

Két könyv előszavából másolok ide egy-egy bekezdést. A múlt század első felében írta Babits Mihály hatalmas áttekintését az európai irodalom történetéről. Így kezdi: „A világirodalom benne él minden olvasójában, s én megpróbálom itt leírni úgy, ahogy énbennem él. Nem csinálok hozzá semmi új tanulmányt. Azt kérdezem magamtól: mi hatott, mi maradt meg bennem?” A múlt század második felében írta Simonyi hatalmas áttekintését a fizika kultúrtörténetéről. Így kezdi: „A jelen könyv írója […] hivatásszerűen fizikával, műszaki tudományokkal és azok pedagógiájával foglalkozva örömét lelte a történelem tanulmányozásában, és ezt az örömét szeretné másokkal is megosztani.”

Mindkét könyv hatalmas ismeretanyagból táplálkozik, az olvasottak mély megértéséről szól. Ennek ellenére nagyon is szubjektív munka mindkettő. Mert abból az örömből táplálkozik, ami a szerzőiket olvasás, tanulás, megértés közben elfogta.

Johann Wolfgang Goethe utolsó versére lehet itt gondolnunk. A tornyában őrködő, éles szemű Lynkeusról szól (Ballagi Zsigmond fordítása).

Lynkeus, a toronyőr

Én nézni születtem,

vagyok, aki lát,

tornyomé a lelkem,

de szép a világ.

Messzire látok,

s szemem itt kutat,

a csillagvilágot,

erdőn a vadat.

Mindenben azt látom,

a díszt, mi örök,

s mert tetszik világom

így megbékülök.

Boldog szemeim, ti,

volt oly sok a kép,

megeshet már bármi,

minden csodaszép.

A látás gyönyörűségét köszöni A fizika kultúrtörténeté-nek minden olvasója.
 

Kulcsszavak: fizikatörténet, művelődéstörténet, elméleti fizika

hőszubsztancia

kinetikus elmélet