|
|
2013. október 8-án jött a hír, hogy a 2013. évi
fizikai Nobel-díjat két elméleti fizikus, a belga François Englert
és a brit Peter W. Higgs (1. ábra) kapta „annak a jelenségnek
elméleti előrejelzéséért, amely megmagyarázza az elemi részecskék
tömegének eredetét, és amelynek érvényességét az elmúlt évben
megerősítette a CERN Nagy Hadronütköztetőjének (LHC) ATLAS- és
CMS-kísérletei által talált új részecske felfedezése”. Mit jelent ez
az indoklás? Mit jelentenek az elemi részecske és tömeg fogalmak?
Mindkettőről van hétköznapi elképzelésünk, de vajon egybeesnek-e
azzal, amit a tudomány ért rajtuk?

1. ábra • François Englert (balról) és Peter Higgs
(jobbról) 2012. július 4-én, a CERN-ben az új részecske
megfigyelésének bejelentésekor.
Amikor a gyümölcsösnél vásárolunk egy kilogramm almát,
tulajdonképpen anyagmennyiséget kérünk. Jól tudjuk, hogy a tömeg és
az anyagmennyiség kapcsolatban állnak egymással, hiszen ha kétszer
nagyobb tömegű almát kérünk, akkor kétszer tovább fogyaszthatjuk. A
kívánt tömeg meghatározása pedig mérlegen történik, amelynek
működése valójában több fizikai törvény együttes alkalmazásán
alapszik. Többek között azon, hogy tudjuk, a Föld a testek tömegével
arányos vonzóerővel hat a testekre. Hétköznapjaink nyugodt
megéléséhez ennyi ismeret elegendő is. Azonban rögtön bajba jutunk,
ha e gondolatokat valamely szélsőséges irányba elkezdjük
kiterjeszteni.
Tekintsünk például egy kb. 10 cm oldalélű kockát
valamely folytonosnak látszó anyagból, például jégből, amelynek
tömege pontosan egy kilogramm. Ha feleannyi jégre van szükségünk,
akkor a tömböt megfelezzük, közülük egynek a tömege fél kilogramm.
Meddig folytatható ez az eljárás? Néhány vágás után akadályba
ütközünk. Hamarosan nem lesz a mérlegünk elegendően pontos, hogy meg
tudjuk mérni, az új fél darab tömege valóban fele-e az eredetinek.
Így abban sem lehetünk biztosak, hogy az anyag mennyisége valóban
egyenes arányosságban van a tömegével, ha a pici testek irányába
mozdulunk. A hétköznapi tömegfogalom nem alkalmazható nagyon nagy
testekre sem, hiszen a Föld tömegét úgy nem lehet meghatározni, hogy
mérlegre tesszük, de a Nemzetközi Űrállomáson még egy fogkefe
tömegét sem. Ahhoz, hogy olyan, talán kicsit szokatlan kérdésekre,
hogy Mekkora a Föld tömege?, vagy Mekkora egy elektron tömege?, vagy
Hogyan lehet meghatározni egy liter víz tömegét a Marson? válaszolni
tudjunk, e fogalmakat olyan tudományos igénnyel kell meghatározni,
hogy kérdéseinkre minden körülmények között választ tudjunk adni,
illetve meg tudjuk fogalmazni, hogy milyen körülmények között nem
alkalmazhatóak ismereteink a válaszok megadására.
Mai világunkban a kényelmet szolgáló eszközök
túlnyomó többsége a részecskék fizikájának megértését célzó
erőfeszítések „mellékterméke”. A „legkisebb” jelentése korról korra
változik, az észlelőberendezéseink felbontásától függ. Amíg a fényt
használtuk a mikrovilág felderítésének eszközeként, a legkisebb
közvetlenül látható szerkezet a mikrométeres tartományba esett.
Ennél kisebb méretekről is lehetett ismereteket szerezni, közvetett
módon a spektroszkópia felhasználásával. Ehhez már szükség volt egy
matematikai modellre is, amelynek segítségével kapcsolatot lehet
teremteni a mért sugárzási spektrum és például az atom szerkezete
között. A korszakot jellemző legkisebb méretek az atomi méretek
voltak.
A mikrovilág megismerésében áttörést jelentett az a
felfedezés, hogy nem csak fényt, hanem részecskéket is lehet apró
szerkezetek felderítéséhez használni. A közvetlen megfigyelésnek
részecskére alapuló eszköze az elektronmikroszkóp, amellyel
nanométeres tartományban lehet az anyag szerkezetét feltérképezni.
Ennél kisebb méretek feloldásának eszköze a részecskegyorsító, amely
ismét közvetett ismereteket szolgáltat. Használatához ismét
matematikai modellre van szükség, amelynek segítségével számszerű
becslést lehet adni részecskeütközéses események különböző
végállapotainak gyakoriságára. A modell jóságát a valódi
kísérletekben bekövetkező végállapotok megszámlálásával lehet
ellenőrizni. A 20. század elején így sikerült Ernest Rutherfordnak
munkatársaival felfedezni az atommagot. Aranyfóliát bombáztak hélium
atommaggal. A kísérlet értelmezése vezetett az atomról alkotott
képünkhöz: a hihetetlenül pici, femtométeres (10-15 m) nagyságú
atommag körül elektronok keringenek a mag méretéhez képest akár
óriási távolságra is: az atom százezerszer nagyobb a magjánál (ha
futballpálya méretűnek képzeljük az atomot, az atommag
gombostűfejnyi a közepén).
Robert Hofstadternek, a Rutherfordéhoz hasonló
összeállítású kísérletekkel sikerült rájönnie, hogy az atommag is
tovább bontható protonokra és neutronokra (összefoglaló néven
barionokra). Ebben a kísérletben a bombázó részecske nagy energiára
gyorsított elektron volt. (Fénysebességhez közeli sebességgel mozgó
részecske gyorsításakor nem a sebessége nő, hanem az energiája.)
Hasonló szóródásos kísérlettel azt is felfedezték, hogy a proton és
neutron sem elemi részecske, hanem kvarkokból épül fel. A proton két
darab u és egy d, míg a neutron két d és egy u kvarkból áll. Az
általunk ismert anyag felépítéséhez tehát három eleminek ismert
részecske szükséges: u és d kvark, valamint elektron. A 20. század
közepén azonban a kozmikus sugárzásban, majd később laboratóriumi
kísérletekben jó néhány új, részben az ismert barionokra, részben az
elektronokra hajazó részecskét találtak. Kiderült, hogy a barionokra
hasonlító részecskék két nagy csoportba sorolhatók. Az egyikben
három kvark kötött állapotai találhatók (ezek a barionok), a
másikban pedig egy kvark és egy antikvark kötött állapota (ezek a
mezonok). A barionok és mezonok tömege a részecskék között
viszonylag nagy, ezért ezeket összefoglaló néven hadronoknak
nevezik. Az elektronra hasonlító részek mind elemiek és viszonylag
könnyűek, ezek neve lepton. (2. ábra)
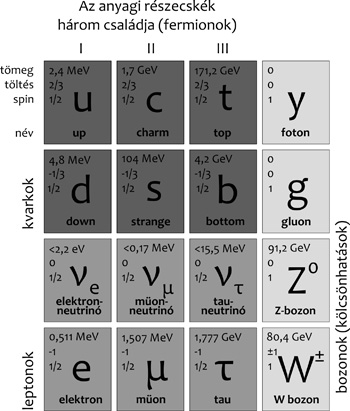
2. ábra • A standard modell elemi
részecskéi: balról jobbra három oszlopban az építőkövek három
családja, a felső két sorban a kvarkpárokkal, az alsó sorban a
leptonpárokkal. Az atomok az első oszlop elektromosan töltött
részecskéiből épülnek fel. A negyedik oszlopban vannak az erőket
közvetítő részecskék, a nulla tömegű fotonok és gluonok, és a nehéz
W és Z bozonok. A táblázatban nincs feltüntetve a közelmúltban
felfedezett Higgs-bozon.
Az elemi részecskéket erők tartják össze, rendezik
változatos kötött állapotokba. Az erőket mezők közvetítik. E mezők
közül az elektromos és mágneses mezővel már mindenki találkozott.
Hatásukra az elektromos töltéssel bíró részecskék lendülete
megváltozik, tehát erővel hatnak rájuk. Minthogy az elektromosan
töltött részecske önmaga is mező forrása, így a töltött részecskék
mező közvetítésével lépnek kölcsönhatásba. Az elektromágneses erőt
közvetítő sugárzásról tudjuk, hogy önmaga is képes lendületet és
energiát szállítani. Gondoljunk csak a nap sugárzására, amely
bőrünket melegíti. Az ilyen tulajdonságú sugárzást nevezzük mezőnek.
Négyféle alapvető kölcsönhatást ismerünk a
természetben: tömegvonzás, elektromágneses, gyenge és erős
kölcsönhatások. Az első kettővel találkozunk a makroszkopikus
világunkban is. A gyenge kölcsönhatás felelős az anyag radioaktív
bomlásáért. Az erős kölcsönhatás csak a kvarkok között hat, és köti
azokat hadronokba. A tömegvonzás a többi háromhoz képest
elhanyagolhatóan pici, így az elemi részek világában nem játszik
szerepet. Esetében az erőhöz köthető mezőt közvetlenül nem sikerült
kimutatni. A másik három kölcsönhatás esetében a mező létezéséről
annak elemi megnyilvánulásának észlelése segítségével győződhettünk
meg. Egy mező elemi megnyilvánulása meghatározott energiát és
lendületet szállító részecske, például a foton. Ugyanígy az elemi
anyagrészecskék is anyagmezők elemi megnyilvánulásának tekinthetők.
A matematikai modell, amelynek segítségével a részecskeütközések
végállapotainak gyakorisága megbecsülhető, az anyag- és erőmezők
kvantumelmélete. E mezők kitöltik a teret, elemi megnyilvánulásaik a
részecskék.
A mezők kvantumelmélete bonyolult matematikai
egyenletekkel írható le, amelyek megjegyzésére csak annak van
esélye, aki napi szinten foglalkozik velük. Elegendően hosszasan
tanulmányozva őket, rájöhetünk, hogy a bonyolult egyenleteket
különleges szimmetriatulajdonságok jellemzik. A szimmetriák egy
része könnyen érthető. Azt fejezik ki, hogy a tér és idő kezdőpontja
szabadon megválasztható. Hasonlóan szabadon választhatjuk
koordináta-rendszerünk tengelyeinek irányát. Érezzük, hogy ennek így
is kell lennie, hiszen egy részecskeütközési kísérlet kimenetele nem
függhet
|
|
|
attól, hogy Genfben vagy Debrecenben végezzük el,
attól sem, hogy mikor, és attól sem, hogy milyen irányból tekintünk
rá. E választási szabadságot az elméletnek is tükröznie kell.
A 20. század végére így alakult ki a
részecskefizikai standard modell (SM). A SM olyan mezők
kvantumelmélete, amelyeknek részecskéit pontszerűnek képzeljük, mert
az eddigi eszközeink feloldóképességének határán belül nem találtunk
semmilyen kisebb szerkezetre utaló nyomot. 2012-ig kétfajta elemi
részecskét, építőköveket (például elektron) és a köztük fellépő
erőket közvetítő részecskéket (ragasztókat, mint például a foton)
ismertük. Érdekes megfigyelés, hogy az építőkövek mindegyike
fermion, a ragasztók pedig bozonok. (A fermionok perdülete ½, a
bozonoké pedig 1 a redukált Planck-állandó egységében mérve.) A
fermionok három családba csoportosíthatók. Egy családhoz tartozik
egy kvarkpár és egy leptonpár. A párok tagjainak elektromos töltése
éppen egy elektron töltésével különbözik. A családok egymásnak
ismétlődései ugyanazokkal a tulajdonságokkal, csupán a részecskék
tömege különbözik.
Hoppá! Mit is értünk egy részecske tömegén? Az
nyilvánvaló, hogy még stabil részecskét sem lehet mérlegre tenni,
nemhogy bomlót, amely a másodperc törtrésze alatt más részecskékké
alakul. Iskolai tanulmányaink szerint „a tömeg a testek
tehetetlenségének mértéke”. A tömeg tudományos igényű meghatározása
még hétköznapi testek esetén is bonyolult. Legyen itt elég annyi,
hogy más testekkel kölcsönhatásba kerülő adott próbatest
sebességének megváltozása a tömegével fordítva arányos. Az elemi
részecskék tömegét is úgy lehet értelmezni, mint a részecskét
jellemző olyan paramétert, amelynek nagysága befolyásolja, hogy mi
történik a más részecskékkel kölcsönhatásba kerülő elemi
részecskével. Tehát függ tőle a részecskeütközések kimenetele.
De térjünk vissza az elemi részek elméletéhez. A SM
mezőelméletének vannak olyan kevéssé kézzelfogható szimmetriái is,
amelyek nem a téridő kezdőpontjának vagy a koordinátatengelyek
irányításának szabad választásával, hanem a mezők más
tulajdonságának szabad választásával kapcsolatosak. Például az egy
családba tartozó kvarkpár tagjait egymásba alakíthatjuk, az
egyenletek ettől nem változnak. Ugyanez a szimmetria vonatkozik a
leptonokra is. Szaknyelven azt mondjuk, hogy az egyenletek nem
változnak a „belső tér” forgatásakor.
A szimmetriaelvekre épülő elmélet sokkal
egyszerűbben megjegyezhető. Elég csak a szimmetriát megjegyezni, az
egyenletek szinte maguktól adódnak. Hasonlóan ahhoz, mint a
tetszőleges irányítású tengely körüli elforgatással szemben
szimmetrikus test, azaz a gömb egyetlen adattal, a sugarával
egyértelműen megadható. A hasonló, de a forgatásokkal szemben nem
szimmetrikus emberfej pontos leírásához rengeteg adatra van szükség.
A belső térbeli forgatásokkal szemben szimmetrikus SM is nagyon
kevés adattal megadható, de van vele egy nagy probléma.
Nyilvánvaló, hogy ha a részecskéknek van tömegük,
akkor az egymásba forgathatóság szimmetriája sérül. A SM
szimmetriákra épülő elméletében a részecskéknek nem lehet tömegük.
Márpedig van, sőt mint fentebb említettük, a családok között éppen a
részecskék különböző tömege tesz különbséget. Ez az a pont, amikor
az olvasó joggal vág közbe: Tessék? Hogyan lehet az elmélet
egyszerre szimmetrikus is, és a benne szereplő részecskéknek tömegük
is? Nos, e kérdés megválaszolásáért adták 2013-ban a fizikai
Nobel-díjat.
Természetesen elfoglalhatnánk azt az álláspontot
is, hogy a részecskéknek van tömegük, így a szimmetriákra alapuló
elmélet nem lehet helyes. Azt csupán a lusta elméleti fizikusok
találták ki, mert nem tudták megjegyezni a bonyolult egyenleteket.
Ez az álláspont teljesen elfogadható, noha nem magyarázná meg azokat
a kísérleti megfigyeléseket, hogy különböző részecskékkel lejátszódó
bizonyos folyamatok gyakorisága miért azonos. A szimmetrikus
elméletben ez kézenfekvő, hiszen a részecskék egymásba forgatásával
a szimmetrikus elmélet nem változik. Az igazi adu ász a szimmetrikus
elmélet mellett a 2012-ben felfedezett új részecske.
1964-ben előbb Robert Brout és François Englert,
majd két hónappal később, tőlük függetlenül Peter W. Higgs
jelentettek meg egy-egy közleményt egy olyan jelenség matematikai
leírásával, amely lehetővé teszi, hogy egy szimmetrikus
kvantum-mezőelméletben hogyan lehet az elemi részecskék tömegét
értelmezni. A kulcs egy különleges tulajdonságú mező (amelyet később
a fizikusközösség Brout-Englert-Higgs-mezőnek, röviden BEH-mezőnek
keresztelt) létezésének feltételezése. A többi mező nagyságának
várható értéke üres térben nulla. Nem úgy a BEH-mezőé, amelynek
értéke még üres térben sem nulla. A standard modellben szereplő
nulla tömegű részecskéknek a speciális relativitáselmélet szerint
fénysebességgel kellene mozogniuk, és így nem képezhetnének olyan
kötött rendszert, mint például egy atom, tehát mi sem létezhetnénk.
A részecskék azonban kölcsönhatnak a mindent kitöltő BEH-mezővel,
ami mintegy „lelassítja” azokat. A lassulás mértéke következetesen
értelmezhető úgy, mintha a részecskéknek tömegük lenne. Ha a
BEH-mező hirtelen megszűnne, a részecskék fénysebességgel
szétszaladnának, és a világban mindenféle szerkezetű anyagi
csoportosulás megszűnne. A BEH-mező segítségével az egyenletek
belsőtérbeli forgatásokkal szembeni szimmetriája megőrizhető úgy,
hogy a szimmetria számunkra láthatatlanná válik (a részecskék tömege
miatt).
Jelenlegi világképünk szerint a Világegyetem az
ősrobbanásban keletkezett szimmetrikus állapotban, amelyben a
részecskéknek nem volt tömegük. A BEH-mező is szimmetrikus
állapotban volt, azaz üres térben értéke nulla. Úgy lehet ezt
elképzelni, mint egy borospohárba tett golyó, amelynek a
legalacsonyabb energiájú állapota (a mezőelméletben ez az üres tér)
a pohár közepén, legalul van. Itt a golyó stabil egyensúlyi
állapotban van, ha kitérítjük egyensúlyából, és magára hagyjuk,
akkor visszatér oda. Képzeljük most el, hogy a golyó legalul van,
amikor hirtelen középen kinő egy, a pohár függőleges
forgástengelyére nézve forgásszimmetrikus púp. A golyó továbbra is
egyensúlyban marad, de ez az egyensúly labilis. Bármilyen kicsi
hatás kitéríti a golyót egyensúlyi helyzetéből, az legördül a púp
oldalán a gödörbe, véletlenszerűen választott irányba. (3. ábra)
Az új alapállapot sérti a forgásszimmetriát. A BEH-mező értéke
pedig a legkisebb energiájú állapotban sem lesz nulla. Ezt a
jelenséget nevezik spontán szimmetriasértésnek, amelynek
kvantum-mezőelméleti megfogalmazásáért kapott Joicsiró Nambu
2009-ben megosztott fizikai Nobel-díjat. De akkor mit díjaztak
2013-ban?
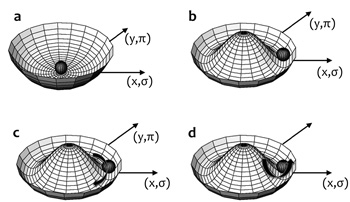
3. ábra • A Higgs-potenciál modellezése:
a – szimmetrikus fázis; b – szimmetriasértett
fázis;
c – Goldstone-gerjesztés a sértett fázisban;
d – Higgs-gerjesztés a sértett fázisban.
A pohárbeli golyónak kétféle elemi gerjesztése van:
egy sugárirányban, és egy arra merőlegesen, a pohárbeli körkörös
gödör mentén. Az utóbbihoz nincs szükség energiabefektetésre, hiszen
a gödör alján mindenhol ugyanakkora a golyó helyzeti energiája. A
mezőelméletben az ennek megfelelő elemi gerjesztés a nulla tömegű
ún. Goldstone-részecske (létezésük lehetőségét Jeffrey Goldstone
jósolta meg). Sugárirányban azonban energiát kell befektetni a golyó
kimozdításához. A BEH-mezőelméletben az ennek megfelelő elemi
gerjesztés a tömeges Higgs-bozon. A pohárbeli púp kinövésének
megfelelő változás a BEH-mezőnek a Világegyetem hűlése miatt
bekövetkező halmazállapot-változása (ahhoz hasonlóan, ahogy a víz
megfagy). A halmazállapot-változás olyan BEH-mezőt kíván, amelynek
négy elemi gerjesztése van. Ezek közül spontán szimmetriasértés
során háromnak nem lesz tömege – ezek a Goldstone-bozonok, egynek
pedig lesz, ez a Higgs-bozon. Az ún. BEH-mechanizmus azt mutatja
meg, hogyan egyesül az eredetileg nulla tömegű, a gyenge
kölcsönhatást közvetítő három részecske és a három Goldstone-bozon,
és lesz belőlük három tömeges, kísérletileg megfigyelhető bozon (W+,
W- és Z). E mechanizmus elméleti megjóslásáért ítélték meg az idei
díjat.
Vajon miért éppen most, közel ötven évvel az
elméleti jóslat után díjazták az eredeti munkákat? A szimmetriákra,
azok spontán sérülésére és a BEH-mechanizmusra épülő SM sok jóslatát
nagy pontossággal igazolták a mérések az elmúlt fél évszázadban,
különösen a múlt század utolsó évtizedében működő nagy
elektron-pozitron gyorsító kísérletei. Nem sikerült azonban
megfigyelni az elmélet jóslatát, a nullánál nagyobb tömegű
Higgs-bozont. Miért? Azért, mert az elmélet csak annyit jósolt, hogy
a tömege nem nulla, de azt nem, hogy mennyi. Így a keresésére
irányuló erőfeszítések ahhoz hasonlíthatók, hogy egy homokkal
megtöltött versenyuszodában kell találnunk néhány különleges
homokszemet, amelyek például tökéletes gömb alakúak, de a méretükről
fogalmunk sincs. A 21. század technikájára volt szükség ahhoz, hogy
a keresés sikerrel járjon. A CERN LHC gyorsítójának kísérletei
másfél ezerbillió proton–proton ütközés végállapotát vizsgálva csak
statisztikusan, de hét 9-es (99,99999%-os) biztonsággal bizonyítani
tudták egy soha korábban nem észlelt részecske létezését, amelynek
tulajdonságai a SM által jósolt Higgs-bozon tulajdonságaival
egyeznek.
A Higgs-bozon felfedezése igazolja a BEH-mező
létezését és az elemi részek tömegének forrását. Mindez az elemi
részecskékre vonatkozik. A mi tömegünk túlnyomó többségét adó
barionok nem elemiek, és tömegük jelentős részének nem a BEH-mező a
forrása. A BEH-mező nélkül azonban a barionokat alkotó kvarkoknak
nem lenne tömegük, és így nem tudnának kötött rendszert alkotni,
tehát végső soron mi sem létezhetnénk.
Kulcsszavak: részecskefizika, kölcsönhatások elmélete, tömeg
eredete, Higgs-bozon, Nobel-díj
|
|