Globális klimatológiai változások hatása
a nehézségi erõtérre, és annak mûholdas
észlelési lehetõségei
Földváry Lóránt
PhD, tudományos fõmunkatárs
MTA–BME Fizikai Geodéziai és Geodinamikai Kutatócsoport
fl ![]() sci . fgt . bme . hu
sci . fgt . bme . hu
Összegzés
A Föld inhomogén tömegeloszlása meglehetõsen komplex nehézségi erõteret hoz létre, mely ráadásul a Föld folyamatos tömegátrendezõdései miatt állandó változásban van. A Föld nehézségi erõterét, illetve annak idõbeni változásait észlelve az azt kialakító tömegeloszlásra, illetve annak átrendezõdéseire következtethetünk. A földi rendszer tömegátrendezõdéseinek nagy része kapcsolatot mutat az éghajlattal vagy annak idõbeli változásaival. A tömegeloszlással járó folyamatok elemzésére globális megoldást kínálnak a gravimetriai mûholdak. Cikkünkben az éghajlatviszonyok észlelésének eddigi mûholdas módszereit ismertetjük, majd évtizedünk legjelentõsebb geodéziai fejlesztésének, a gravimetriai mûholdaknak szerepét vizsgáljuk a globális éghajlatviszonyok észlelésében, és utalunk várható szerepükre az éghajlatváltozások diagnosztizálásában.
1. A Föld tömegátrendezõdései
Jelenlegi ismereteink alapján a Föld számottevõ tömegátrendezõdései a geoszférában (ott is a felsõ köpenyben és a kéregben), a hidroszférában (beleértve a krioszférát is), valamint az atmoszférában zajlanak le. Az I. táblázatban a Föld fenti felbontás szerinti jelentõsebb tömegátrendezõdéseit gyûjtöttük össze (Ilk et al., 2005). (1. táblázat)
A táblázatból a hirtelen, rövid idejû erõhatások által okozott egyszeri, dinamikus tömegátrendezõdésektõl, nevezetesen a földrengésektõl, a vulkánkitörésektõl és a földcsuszamlástól eltekintve valamennyi említett folyamat az éghajlat alakulásáért felelõs tényezõ.
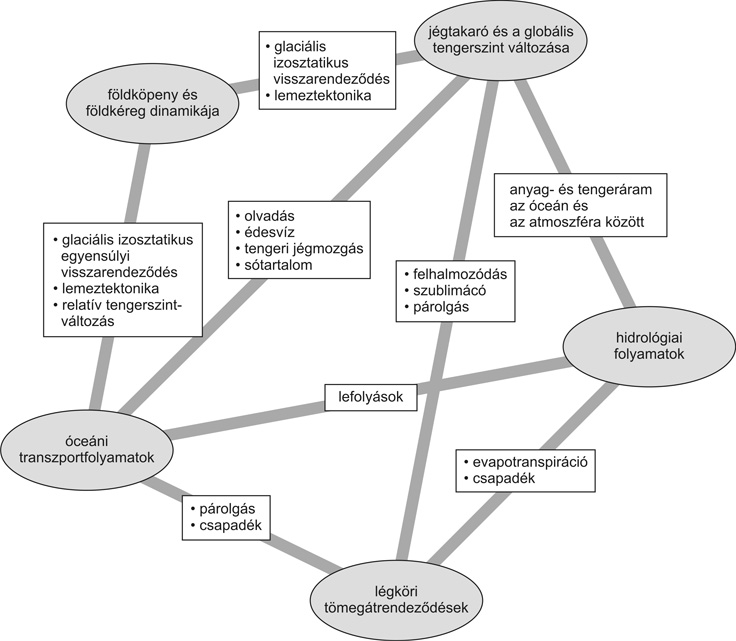
A tömegátrendezõdések jellemzõen (már csak anyagi minõségi különbség okán is) nem lépnek ki egy-egy „tározóból”, azok határain belül mûködnek. Itt elsõsorban az óceánokon belüli tömegáramokra, az atmoszféra légkörzésére vagy a földköpeny áramlásaira gondolunk, amelyek a tömegáramok méreteihez képest kis mértékben kavarodnak. Nyilván azért teljes elszigeteltségben egyik összetevõ sincs jelen. Az 1. ábra a nagyobb tömegáram tartályokat (ahol az eljegesedéseket és a kontinentális vízháztartást elvi megfontolásból külön szegmenskent ábrázoljuk), valamint a köztük kialakuló tömegáramokat mutatja.
Mint már jeleztük, az ábrán is bemutatott tömegáramok mindegyike az éghajlattal szoros viszonyban áll, a kialakult éghajlatviszonyokért felelõs. Észlelésük és értelmezésük fontos a földi éghajlatviszonyok globális megértéséhez.
2. Éghajlatjellemzõ jelenségek
mûholdas észlelése
Az éghajlattal kapcsolatos jelenségek globális észlelése az altimetriai mûholdakkal a 90-es évek elején kezdõdött (Seeber, 1993). Kialakításukhoz a GPS mûholdas helymeghatározó rendszer kiépülése elengedhetetlen feltétel volt. Az altimetriai mûholdak után a következõ nagy lépést 2000-ben az elsõ gravimetriai mûhold fellövése jelentette. Ezzel a globális éghajlat fizikai változásainak észlelési hálózata egy fontos szegmenssel kibõvült. A 2. ábrán az éghajlattal kapcsolatos fizikai jelenségek észlelésének jelenleg használatos mûholdas technikáit mutatjuk.
Az éghajlatviszonyok feltérképezésében részt vevõ mûholdas észlelési technikák ismertetését adjuk a következõkben, elsõsorban a cél szemszögébõl fontos tulajdonságokra koncentrálva.
2.1 Helymeghatározó rendszerek
A globális mûholdas rendszerek mûholdjai napjainkra nagy pontosságú vonatkoztatási rendszereket alkotnak a Föld körül, amely mûholdakra tetszõleges földfelszíni pontból távolságot mérve, a Föld felszínén a helyzetünk nagy pontossággal meghatározható. A mûholdak nagy pályamagassága lehetõvé teszi a náluk alacsonyabban keringõ mûholdak folyamatos pályameghatározását is. A pálya folyamatos ismerete pedig lehetõséget nyújt egy mûhold folyamatos méréseinek térbeli pontos elhelyezésére vagy geometriai méretek meghatározására, például a Föld felszínére végzett folyamatos távolságmérésekbõl (ún. altimetria).
A globális helymeghatározó rendszerek közül a GPS-rendszer a 80-as évek második felétõl mérnöki használatra alkalmassá vált, majd 1994-re teljesen kiépült, míg a GLONASS teljes rendszere 1996-ra készült el (Ádám et al., 2004). A felhasználás szempontjából a GPS-nek van nagyobb gyakorlati jelentõsége, és ez igaz a mûholdas alkalmazásokra is.
2.2 Óceántopográfia mûholdas
altimetria segítségével
A mûholdas altimetria alapelvét szemlélteti a 3. ábra. A mûhold mikrohullámú jelet bocsát ki fedélzetérõl, ami a víz felszínérõl jól verõdik vissza, és a visszavert jelet észleli. A jel terjedésébõl a távolság könnyen meghatározható (Seeber, 1993). A GPS-mûholdakra végzett folyamatos helymeghatározás lehetõséget ad a vízfelszínek geometriájának kvázi folyamatos mérésére. A radar-altimetria legsikeresebb megvalósulása a TOPEX/Poseidon mûhold (1992-tõl napjainkig), amely segítségével az óceánok dinamikus topográfiáját elõször lehetett globálisan meghatározni. A folyamatos mérések következtében az óceánfelszín geometriájának idõrõl idõre nyert pontos ismerete a globális óceáni változások feltérképezésének nagyon fontos mérföldkövét jelenti.
A TOPEX/Poseidon projekt számára további elõrelépést jelentett a Jason–1 nevû mûhold 2001-es fellövése. A mûhold egy ideig a TOPEX/Poseidonhoz közel, azzal teljesen megegyezõ pályán keringett, és végzett altimetriai méréseket, amelyek alapján a mûhold mérési képességeit a TOPEX/Poseidonhoz képest kalibrálták. Ezután a TOPEX/Poseidonnal „párhuzamos” pályára állították, ezzel a két mûhold megduplázta a meghatározott topográfia felbontását, gyakorlatilag idõegység alatt kétszer annyi területet térképeznek fel, mint amennyit a TOPEX/Poseidon egyedül képes. A radar-altimetria sikerének tudható be, hogy 2008-ra már tervezik a Jason–1 folytatását, az OSTM-et.
2.3 Jégtakarótopográfia észlelése
A jégtakaró észlelésének alapelve teljesen megegyezik az óceán felszínére végzett altimetriai mérésekével, csak szakmatörténetileg úgy alakult, hogy az altimetria kifejezés alatt csak az óceánok topográfiájának meghatározását értjük. A jégtakaró által visszavert mikrohullámú jel frekvenciája (nyilván) eltér valamelyest az óceáni altimetriához használt frekvenciától, de ez az alapelven nem változtat.
A jégtakaró észlelése már 1991-ben megindult az ERS–1 mûholddal (lásd 2.4 pont), mégis, pusztán jégtakaró meghatározására irányuló mûhold nem mûködött egészen 2003-ig. Ekkor az IceSat kezdte meg tevékenységét, amelyet azóta nem követett folytatás, bár említést kell tennünk a Cryosat projektrõl, amelynek fellövése során sajnálatos módon felrobbant a hordozórakéta, 2005-ben.
2.4 Kombinált altimetriai megoldások
Az altimetria hajnalán, 1991-ben a jégtakaró és az óceán topográfiájának meghatározására egyaránt alkalmas ERS–1 mûhold indult útnak, amely körülbelül 2000-ig nyújtott használható eredményeket (tervezett küldetése 1996-ig tartott). Ezt 1995-tõl az ERS–2 egészítette ki (majd váltotta fel a fõ tevékenységét), amit 2002-ben az ENVISAT követett. A kombinált megoldások csökkentik a költség/hasznos teher arányt, ám ez az egyes részfeladatok optimális kivitelezése szempontjából engedményeket követel meg.
2.5 Gravimetriai mûholdak
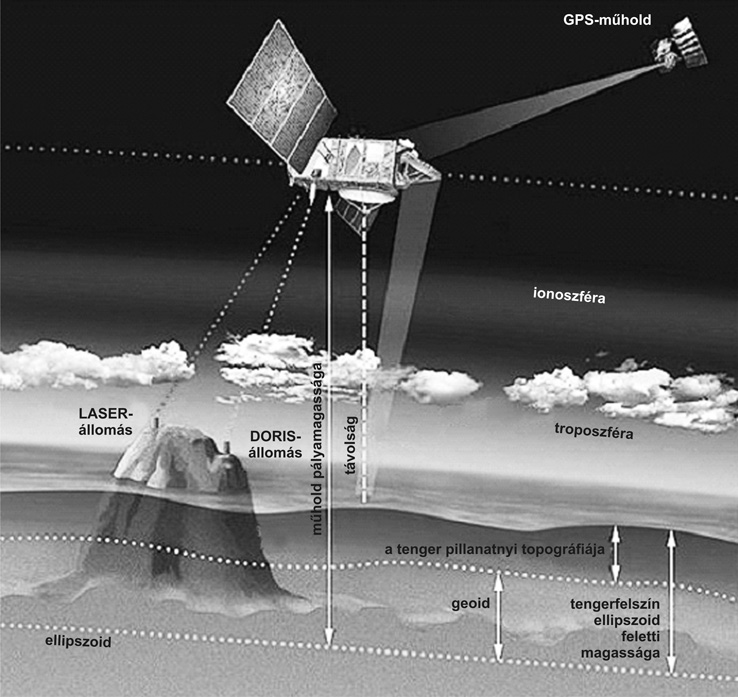
Látható, hogy az eddig ismertetett megoldások mindegyike geometriai méretek, felszínek topográfiájának leírását adja. A geometriai ismeretet a tömegeloszlásra vonatkozó ismeretekkel egészítik ki a gravimetriai mûholdak (Flury et al., 2006; Földváry, 2004). A tömegeloszlás meghatározásának alapelvét legegyszerûbben a 2000-tõl pályán lévõ CHAMP elnevezésû mûhold kapcsán lehet megmutatni (4. ábra).
Mivel a szabadon esõ mûhold pályáját a nehézségi erõtér alakítja ki, a mûhold pályájának a folyamatos ismeretébõl az azt kialakító erõtérre, tehát a Föld nehézségi erõterére lehet következtetni. A mûhold pályáját a GPS-mûholdakra végzett mérések adják meg, az egyéb, nem gravitációs eredetû erõhatások mérésére pedig (például légköri fékezés) a mûhold fedélzetén elhelyezett gyorsulásmérõ szolgál.
Ugyanezen elvnek kicsit finomított megoldását az 5. ábrán szemléltetjük a GRACE mûholdak kapcsán. Két mûhold kering közel azonos pályán, a CHAMP-hez hasonló elrendezésben. A két mûhold között folyamatosan nagyon pontos távolságmérést végzünk. A távolság változásából a nehézségi erõ-tér térbeli változásaira lehet következtetni.
A mûholdas gradiometria megvalósulását a GOCE-mûhold 2008 szeptemberére várható fellövése jelenti majd. A mûholdas gradiometria elrendezését a 6. ábra mutatja. A mûhold belsejében három pár gyorsulásmérõt helyeztek el egymásra merõleges tengelyek mentén; ez a mûszer a gradiométer. Az alapelv a GRACE alapelvéhez hasonló: egy-egy tengely mentén a gyorsulásmérõk tömegeinek egymáshoz képesti elmozdulásából a nehézségi erõtér változására következtethetünk az adott tengely irányában. A három egymásra merõleges tengely a nehézségi erõ változásainak térbeli meghatározását teszi lehetõvé. További különbséget jelent a GRACE-hez képest a mérési elrendezés méretaránya: a jóval kisebb méretek miatt a GOCE a nehézségi erõtér változásának jóval kisebb frekvenciájú összetevõinek meghatározására hivatott.
3. A gravitációs tér éves és féléves változásai GRACE-mérések alapján
A fent említett három gravimetriai mûhold közül ténylegesen az éghajlat, illetve az éghajlatváltozások meghatározására legnagyobb segítséget a GRACE nyújthatja (Földváry, 2007). A GRACE pályáját úgy alakították ki, hogy az éves és a féléves periódusú változásokra legyen érzékeny. Éves és féléves változásokat az atmoszféra, az óceáni tömegáramok (fõleg féléves periódus), valamint a kontinentális hidrológiai folyamatok (fõleg éves periódus) okoznak.
3.1 A GRACE mûholdpár ismertetése
A GRACE mûholdak átlagban 485 km magasságban, közel poláris, és közel körpályán keringenek. A két mûhold közötti mikrohullámú távolságmegváltozás mérésének pontossága 1 µm/s alatt van. Ezzel a mérési elrendezéssel lehetõvé válik, hogy mintegy hónapnyi mérési adatból a globális nehézségi erõteret jó lefedettséggel, nagyon pontosan megismerjük. A havi felbontású modellek pedig a féléves, de fõleg az éves periódusú változások értelmezését teszik lehetõvé.
A Center for Space Research (a Texasi Egyetem ûrkutatóintézete) munkatársai bõ két év idõtartamú nyers GRACE-mérést dolgoztak fel (Tapley et al., 2005). Eredményként húsz darab, közel harmincnapnyi adatból nyert globális nehézségi erõtérmodellt kaptak. A 2. táblázatban a közel hónapnyi hosszúságú modellek egyszerûbb jellemzõit mutatjuk.
A GRACE-modellek az atmoszféra által keltett tömegvonzást nem tartalmazzák, azokat egy globális atmoszféramodell alapján levonták. Erre a korrekcióra azért kerülhetett sor, mert a gyakorlatban az atmoszféra jobban ismert tömegáramokat kelt, mint az óceánok és a hidrológiai folyamatok. Így kontinentális területeken a GRACE-modellek éves változásai fõleg a hidrológiával, míg az óceáni területek az óceáni tömegáramokkal mutatnak egyezést. A GRACE-mérések alapján meghatározott nehézségi erõtér modelleket ebben a tanulmányban a mûhold eddigi eredményeinek elemzésére és szemléltetésére használjuk a következõ pontban.
3.2 A GRACE eredményeinek szemléltetése
3.2.1 A gömbfüggvény-együtthatók éves változásai • A felsõgeodézia számára közismert a nehézségi erõtér gömbfüggvény soros leírása (Biró, 1985):
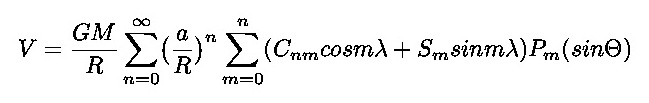
A gömbfüggvénysor matematikailag a nehézségi erõtér kétdimenziós Fourier-soros alakjának felel meg. Az összefüggés gyakorlatilag a Föld nehézségi erõterének potenciálfelületét közel gömb alakú felületként kezeli, és a gömbtõl való eltéréseket kétdimenziós hullámok formájában írja le. A kétszeri szummázás az egyenletben a két dimenzió mentén a hullámhosszak szerinti integrálásnak felel meg. Egy-egy hullámhossz amplitúdóját a Fourier-együttható adja meg (ezeket az együtthatókat a geodéziai gyakorlatban gömbfüggvény-együtthatóknak nevezzük). Mivel a gömbfüggvénysor hullámhosszankénti (frekvencia szerinti) összetevõi ortonormális bázist alkotnak, a komponensek egymástól független tényezõkként kezelhetõk. Az összetevõk függetlensége miatt a nehézségi erõtér egy-egy tulajdonsága valamennyi komponensben, tehát valamennyi frekvencián egyenként nyilvánul meg. Így a teljes nehézségi erõtér éves és féléves periódusú változásai is a nehézségi erõtér minden frekvenciáján nyilvánulnak meg, a gömbfüggvényegyütthatók éves és féléves változásainak formájában.
A GRACE mérései alapján meghatározott nehézségi erõtér modell együtthatóinak idõbeni változásait jelenítjük meg a 7. ábrán. Megjegyzésképpen: a nagyobb indexek a kisebb hullámhosszaknak felelnek meg. A nagyobb hullámhosszakhoz rendszerint nagyobb amplitúdó is tartozik; mondhatjuk ezért, hogy a kisebb indexû együtthatók nagyobb fontosságúak a globális nehézségi erõ-tér kialakításában.
Az ábrákon látható görbék közel kétévi változást szemléltetnek. A földi rendszerben az éves változás amplitúdója nagyobb a fél évesnél, így szemre az éves változást próbálhatjuk meg felfedezni. Ez egyes együtthatók esetén elég szépen észrevehetõ (például C3,0, S4,2 vagy C4,4), ami azt jelenti, hogy adott frekvencián a változásokban ténylegesen éves periódus a domináns. Más együtthatók, így például a C2,0, semmilyen periodikus változást nem mutatnak, ami vagy azt jelenti, hogy a periodikus változások nagyságrendje elhanyagolható az egyéb változásokhoz képest, vagy azt, hogy a mérés geometriai elrendezése nem volt megfelelõ adott frekvencia változásainak feltérképezésére. A C2,0 tag éves változásainak hiánya komoly gyengéje a megoldásnak, hiszen ez az együttható az ábrákon feltüntetett együtthatók közül a legnagyobb amplitúdójú, ez az együttható adja meg a Föld szabályos gömbhöz képesti egyenlítõi lapultságát.
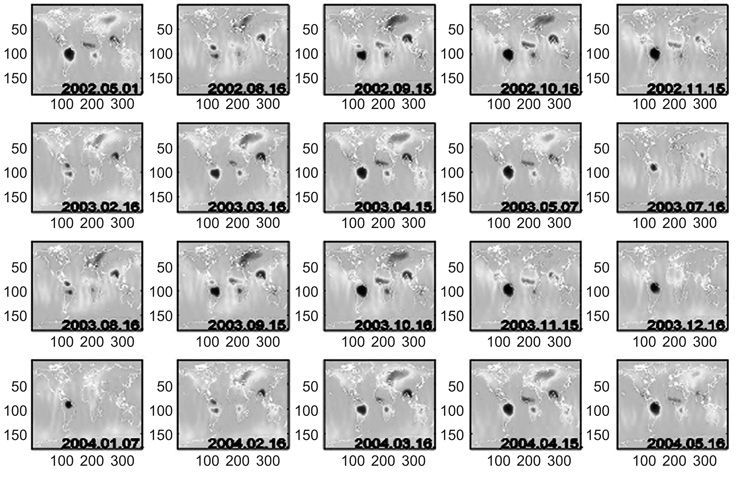
3.2.2 A geoid éves változásai • A nehézségi erõtér szerkezetének geometriai szemléltetésére a közepes tengerszinteknek megfelelõ szintfelületet szokás használni, ez az ún. geoid. A 8. ábrán a teljes Föld geoidváltozásait mutatjuk be. A geoidváltozásokhoz idõpontként a közel hónapnyi idõtartam közepét rendeltük hozzá, és tüntettük fel az ábrák alján.
A 8. ábrán az éves ciklus a legtöbb helyen kiválóan látszik, különösen a kontinentális területeken, ami a hidrológiai folyamatok nagy egyéves periódusával jó összhangban van. Egyes területek jól ismert tömegátrendezõdésekhez kapcsolhatók, így például jól látható az Amazonas vízgyûjtõ medencéjének éves periódusú változása. Ezt a területet külön kiemelve mutatjuk a 9. ábrán. Szintén jellegzetes éves periódus látható az egykori Indokína területén, a Himalája vízválasztótól a Bengáli-öbölbe torkolló folyamok (Gangesz, Brahmaputra, Irrawady stb.) vízgyûjtõ területein. Ezt a 10. ábrán mutatjuk be.
3.3 A GRACE-projekt
várható eredményei és folytatása
A GRACE aktív korszaka elsõ két évének eredményeiben éves változásokat kerestünk vizuálisan. Bizonyos frekvenciákon, illetve bizonyos területeken az éves periódus szépen kivehetõnek bizonyult. A gyakorlatban a kétévi adatsorból nyert éves periódus csak közelítõ becslésnek fogadható el, és egyelõre mindössze az elképzelés hitelesítésére alkalmas. Hidrológiai és oceanográfiai alkalmazások számára hosszabb adatsorra van szükség, amelyek gyûjtése 2008-ig folyamatosan tart.
Az ötéves adatsor elõreláthatólag lehetõséget ad majd az éves és féléves változások értékének jó becslésére, és az ismert éghajlatalakító hasonló periódusú jelenségek elemzésére, a kapcsolódó oceanográfiai és hidrológiai modellek pontosítására. A jelenlegi adatmennyiséggel azonban ez nem lehetséges.
Távolabbi cél a hosszabb periódusú és szekuláris éghajlatváltozások elemzése. Ezekre nagyon közelítõ feltételezéseket az ötévnyi adatsor alapján tehetünk majd, mégsem várhatunk mérvadó eredményeket. Erre az adatsor még hosszabb ismerete szükséges. A GRACE mûholdak az alacsony pályájuk miatt az ötéves várható idõtartamot lényegesen nem tudják megnyújtani, így a folytonos adatsor biztosítása érdekében egy következõ, hasonló elrendezésû projektre lenne szükség. Egy idõben sok szó esett a GRACE-projekt folytatásáról az EX-5 elnevezésû projekt keretében (Watkins et al., 2000). Elõzetesen 2007-es fellövést terveztek, amely megadta volna a szükséges átfedést a két projekt között, azonban a projekt indítását egyelõre elhalasztották. A GRACE jelenleg az ötéves idõtartamán túl is hatékonyan folytatja a tevékenységét, azonban az adatsor hosszú távú folytatására ez nem jelent megoldást.
A tanulmány a Bolyai-ösztöndíj támogatásával készült.
Kulcsszavak: klímaváltozás, földi tömegátrendezõdések, idõben változó nehézségi erõtér, ûrgravimetria, GRACE
IRODALOM
Ádám József – Bányai L. – Borza T. – Busics Gy. – Kenyeres A. – Krauter A. – Takács B. (szerk.), (2004): Mûholdas helymeghatározás. (egyetemi tankönyv) Mûegyetemi, Budapest
Ádám József (2007): Globális Geodéziai Megfigyelõrendszer. Magyar Tudomány. 5, 563–576.
Biró Péter (1985): Felsõgeodézia. (egyetemi jegyzet) Tankönyvkiadó, Budapest
Flury, Jakob – Rummel, R. – Reigber, Ch. – Rothacher, M. – Boedecker, G. – Schreiber, U. (eds.) (2006): Observation of the Earth System from Space. Springer-Verlag, Berlin–Heidelberg
Földváry Lóránt (2004): A 2000-es évek elsõ évtizede: A gravimetriai mûholdak korszaka. Magyar Geofizika. 45, 4, 118–124.
Földváry Lóránt (2007): Az évszakos nehézségi erõtér változások GRACE mûholdas meghatározásának pontossági kérdései, Geodézia és Kartográfia. 59, 8–9, 40–46.
Ilk, Karl-Heinz – Flury, J. – Rummel, R. – Schwintyer, P. – Bosch, W. – Haas, C. – Schröter, J. – Stammer, D. – Zahel, W. – Miller, H. – Dietrich, R. – Huybrechts, P. – Schmeling, H. – Wolf, D. – Götze, H. J. – Riegger, J. – Bardossy, A. – Güntner, A. – Gruber, Th. (2005): Moass Transport and Mass Distribution in the Earth System. GOCE Projektbüro Deutschland, Technische Universität München– GeoForschungsZentrum, Potsdam
Seeber, Günter (1993): Satellite Geodesy. Walter de Gruyter, Berlin, New York, p. 532
Tapley, Byron – Ries, J. – Bettadpur, S. – Chambers, D. – Cheng, M. – Condi, F. – Gunter, B. – Kang, Z. – Nagel, P. – Pastor, R. – Pekker, T. – Poole, S. – Wang, F. (2005): GGM02 – An improved Earth Gravity Field Model from GRACE. Journal of Geodesy. DOI 10.1007/s00190-005-0480-z
Watkins, Michael M. – Folkner, W. M. – Chao, B. F. – Tapley, B. D. (2000): The NASA EX-5 Mission: A Laser Interferometer Follow-on to GRACE. Technical Program and Abstracts of IAG International Symposium GGG2000, Banff, Alberta, Canada
|
GEOSZFÉRA |
HIDROSZFÉRA |
ATMOSZFÉRA |
|
|
|
|
|
földrengés |
óceáni transzportfolyamatok |
globális légkörzés |
|
|
|
|
|
vulkánkitörés |
mélytengeri áramlások |
atmoszferikus árapály |
|
|
|
|
|
tektonikus mozgás |
vízkörforgás |
|
|
|
|
|
|
földcsuszamlás |
árapály jelenségek |
|
|
|
|
|
|
glaciális izosztatikus |
jégtakaró és jégolvadás |
|
|
|
|
|
|
átrendezõdés |
globális tengerszintváltozás |
|
|
|
|
|
|
posztglaciális izosztatikus |
|
|
|
visszarendezõdés |
|
|
|
|
|
|
|
konvekciós áramlások a köpenyben |
|
|
|
|
|
|
|
belsõ mag áthelyezõdése |
|
|
1. táblázat • A Föld jelentõsebb tömegátrendezõdései, tömegáramai.
1. ábra • A földi tömegáramok rendszere
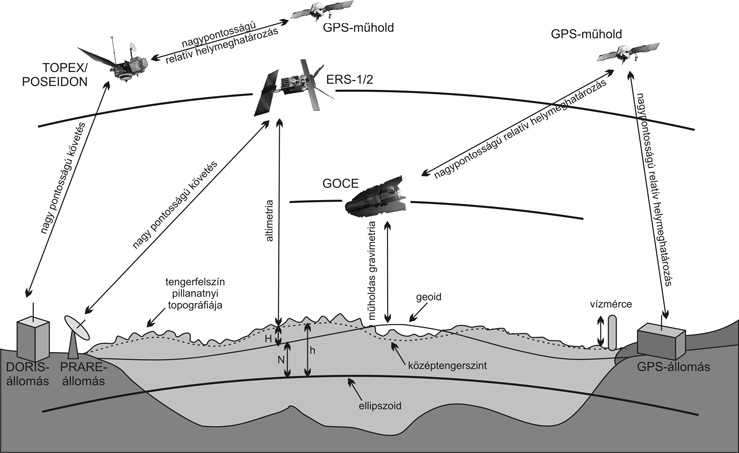 2.
ábra • A globális földmegfigyelõ
rendszer (Global Earth Orbiting Satellite Systems [Ádám,
2007]) mûholdas technikái,
amelyek alapján az éghajlattal kapcsolatos jelenségek
észlelését végzik. N – geoid
unduláció; H – a tengerfelszín
topográfiája; h – közepes tengerszint
ellipszoid feletti magassága (Forrás:
http://tau.fesg.tu-muenchen.de/~iapg/web/index.php
)
2.
ábra • A globális földmegfigyelõ
rendszer (Global Earth Orbiting Satellite Systems [Ádám,
2007]) mûholdas technikái,
amelyek alapján az éghajlattal kapcsolatos jelenségek
észlelését végzik. N – geoid
unduláció; H – a tengerfelszín
topográfiája; h – közepes tengerszint
ellipszoid feletti magassága (Forrás:
http://tau.fesg.tu-muenchen.de/~iapg/web/index.php
)
 3.
ábra • A mûholdas
altimetria alapelve (Forrás:
http://tau.fesg.tu-muenchen.de/~iapg/web/index.php
)
3.
ábra • A mûholdas
altimetria alapelve (Forrás:
http://tau.fesg.tu-muenchen.de/~iapg/web/index.php
)
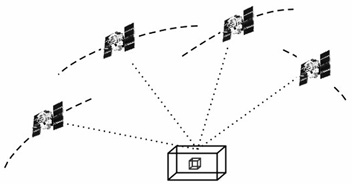 4.
ábra • A CHAMP mûhold
észlelési módszerének elvi sémája
4.
ábra • A CHAMP mûhold
észlelési módszerének elvi sémája
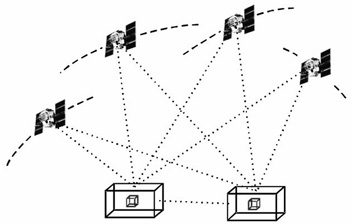 5.
ábra • A GRACE mûholdak
észlelési módszerének elvi sémája
5.
ábra • A GRACE mûholdak
észlelési módszerének elvi sémája
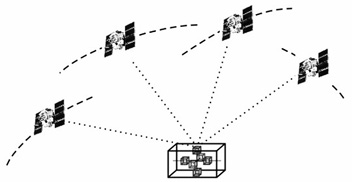 6.
ábra • A GOCE mûhold
észlelési módszerének elvi sémája
6.
ábra • A GOCE mûhold
észlelési módszerének elvi sémája
|
napok adott évben |
napok száma |
értelmezési nap (2002. 01. 01-tõl) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. táblázat • A tanulmányban használt globális nehézségi erõtér modellek jellemzõi
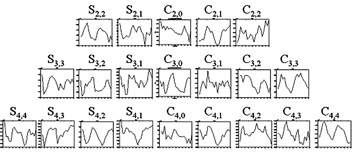
7. ábra • A GRACE-mérések alapján meghatározott gömbfüggvény-együtthatók idõbeni változása
 8.
ábra • A GRACE-mérések alapján
meghatározott geoid képek idõbeni
változása
8.
ábra • A GRACE-mérések alapján
meghatározott geoid képek idõbeni
változása
 9.
ábra • A GRACE-mérések alapján
meghatározott geoid képek idõbeni
változása az Amazonas vízgyûjtõje
környékén
9.
ábra • A GRACE-mérések alapján
meghatározott geoid képek idõbeni
változása az Amazonas vízgyûjtõje
környékén
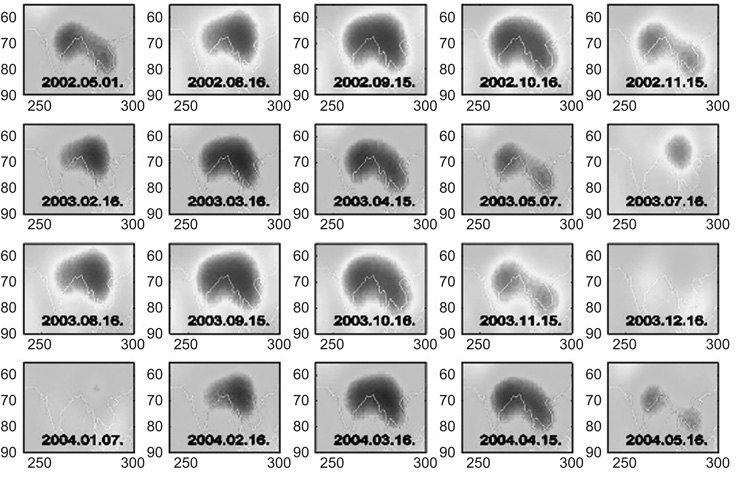 10.
ábra • A GRACE-mérések alapján
meghatározott geoid képek idõbeni
változása Indokína területén
10.
ábra • A GRACE-mérések alapján
meghatározott geoid képek idõbeni
változása Indokína területén
<-- Vissza a 2008/06 szám tartalomjegyzékére
<-- Vissza a Magyar Tudomány honlapra
[Információk] [Tartalom] [Akaprint Kft.]